Ley de Ohm (GIOI)

De Laplace

Revisión a fecha de 15:36 11 mar 2020; Antonio (Discusión | contribuciones)

(dif) ← Revisión anterior | Revisión actual (dif) | Revisión siguiente → (dif)

Contenido

1 Ley de Ohm
- 1.1 Aplicación a un conductor filiforme
2 Resistencia eléctrica
- 2.1 Asociaciones de resistencias
- 2.2 Cortocircuito y circuito abierto
3 Amperímetros y voltímetros
- 3.1 Amperímetros
- 3.2 Voltímetro
4 Condensador real

1 Ley de Ohm

En los apartados anteriores hemos descrito el movimiento de las cargas, sin atender a las causas que lo producen. Para tener en cuenta las causas necesitaríamos o bien medir experimentalmente la corriente como función de otros parámetros, o bien analizar los diferentes modelos de conducción, para ver qué relación teórica hay entre la densidad de corriente y el campo eléctrico (y otras fuerzas aplicadas).

El resultado es que en la gran mayoría de las materiales existe una relación sencilla entre la densidad de corriente y el campo eléctrico en el interior del material. Esta relación es la ley de Ohm:

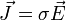
$\vec{J}=\sigma\vec{E}$

donde $σ$ es una propiedad de cada material conocida como su conductividad. Se mide en el SI en siemens/metro (S/m) y es la propiedad física que más cambia de unas sustancias a otras.

Material	$σ$ (S/m)	$ρ$ (Ω·m)
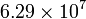
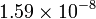
Plata	$6.29\times 10^{7}$	$1.59\times 10^{-8}$
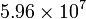
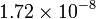
Cobre	$5.96\times 10^{7}$	$1.72\times 10^{-8}$
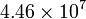
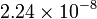
Oro	$4.46\times 10^{7}$	$2.24\times 10^{-8}$
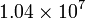
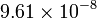
Hierro	$1.04\times 10^{7}$	$9.61\times 10^{-8}$
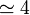
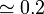
Agua de mar	$\simeq 4$	$\simeq 0.2$
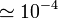
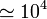
Agua destilada	$\simeq 10^{-4}$	$\simeq 10^{4}$
Goma	$10 - 15 - 10 - 13$	$1013 - 10 15$

A menudo se da como dato la inversa de la conductividad, llamada la resistividad ( $ρ$ o $r$ ), que se mide en Ω·m.

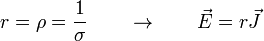
$r=\rho = \frac{1}{\sigma}\qquad\rightarrow\qquad \vec{E}= r\vec{J}$

La ley de Ohm nos dice sencillamente que si las cargas se mueven es porque hay un campo eléctrico que las empuja, aunque debido a la fricción con el material, no es la aceleración, sino la velocidad, la que es proporcional al campo eléctrico.

La ley de Ohm no es una ley universal. Solo se cumple en los llamados materiales óhmicos (que son la mayoría) pero no, por ejemplo, en los plasmas.

La excepción más importante de sistema en el que no se cumple la ley de Ohm es en un generador. Como veremos, en un generador la densidad de corriente va en sentido contrario al campo eléctrico, lo cual es la negación absoluta de la ley de Ohm.

1.1 Aplicación a un conductor filiforme

La ley de Ohm así enunciada no es como suele aparecer en los libros de teoría de circuitos. La razón es que al analizar un circuito no interesa tanto lo que ocurre en cada elemento de volumen, y sí lo que ocurre a nivel macroscópico, mediante magnitudes medibles de forma sencilla como la intensidad de corriente y la diferencia de potencial.

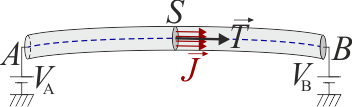
Para llegar a la ley de Ohm tal como se ve en teoría de circuitos consideramos en primer lugar el caso de un conductor filiforme (un hilo), que es aquél que tiene una longitud mucho mayor que su diámetro y que su radio de curvatura. Este hilo va de un punto A a un punto B, siguiendo una cierta curva (no tiene por qué ser una recta). Suponemos que la intensidad de corriente fluye de A a B. Nos preguntamos por la diferencia de potencial entre los dos extremos. Por definición de d.d.p. tenemos que

$V_A- V_B = \int_A^B \vec{E}\cdot\mathrm{d}\vec{r}$

Puesto que en el cable se cumple la ley de Ohm

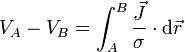
$V_A- V_B = \int_A^B \frac{\vec{J}}{\sigma}\cdot\mathrm{d}\vec{r}$

Al recorrer la curva que constituye un conductor filiforme el desplazamiento va en la dirección del vector tangente

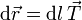
$\mathrm{d}\vec{r}=\mathrm{d}l\,\vec{T}$

Por otro lado, por ser muy estrecho, la densidad de corriente va también en el sentido longitudinal

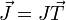
$\vec{J}=J\vec{T}$

lo que nos deja la d.d.p como la integral escalar

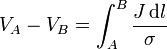
$V_A- V_B = \int_A^B \frac{J\,\mathrm{d}l}{\sigma}$

En el caso de un conductor filiforme se cumple además que la densidad de corriente es la misma en todos los puntos de una sección transversal, de forma que podemos hacer la aproximación

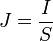
$J = \frac{I}{S}$

siendo $I$ la intensidad de corriente que circula por el cable. Esta intensidad es la misma a lo largo de todo él, por lo que podemos sacarla de la integral y nos queda finalmente

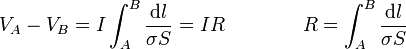
$V_A- V_B = I\int_A^B \frac{\mathrm{d}l}{\sigma S}= IR\qquad\qquad R = \int_A^B\frac{\mathrm{d}l}{\sigma S}$

La cantidad $R$ es la resistencia eléctrica del hilo. Es una integral porque, en principio, la conductividad y la sección pueden ir variando a lo largo del cable. En el caso común de un cable de un solo material con sección constante

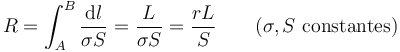
$R = \int_A^B\frac{\mathrm{d}l}{\sigma S} = \frac{L}{\sigma S}=\frac{r L}{S}\qquad(\sigma, S\ \mbox{constantes})$

2 Resistencia eléctrica

Acabamos de ver que en un cable hecho de un material óhmico se cumple una relación de proporcionalidad entre la diferencia de potencial entre sus extremos y la intensidad de corriente que circula por el cable

$V_A-V_B = IR\,$

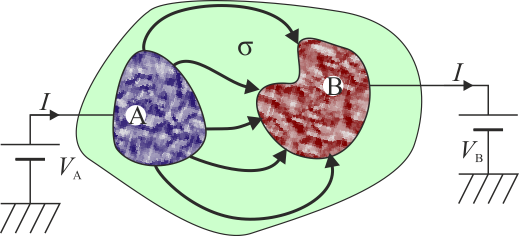
Esta es la llamada ley de Ohm en la teoría de circuitos y es generalizable a gran variedad de situaciones aunque no tengamos un hilo. Siempre que haya dos electrodos entre los cuales se encuentra un material (o materiales) óhmicos, se cumple esta misma relación, aunque el valor de la resistencia será una función complicada de la geometría y los materiales interpuestos.

La resistencia eléctrica se mide en ohmios (Ω) definidos como

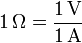
$1\,\Omega = \frac{1\,\mathrm{V}}{1\,\mathrm{A}}$

La ley de Ohm circuital también puede escribirse

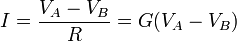
$I=\frac{V_A-V_B}{R}=G(V_A-V_B)$

donde

$G = \frac{1}{R}$

es la conductancia del sistema, medida en siemens (S)

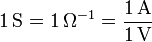
$1\,\mathrm{S}=1\,\Omega^{-1}= \frac{1\,\mathrm{A}}{1\,\mathrm{V}}$

En las expresiones anteriores, para que salgan los signos correctos, si se halla la diferencia de potencial entre A y B, hay que suponer que la corriente va de A a B. Si se da la vuelta a ambas magnitudes, sigue saliendo el resultado correcto, pero si solo se la da la vuelta a una resulta el signo incorrecto.

Un elemento de circuito caracterizado por poseer una resistencia eléctrica se denomina un resistor (del mismo modo que uno que tiene capacidad es un condensador), aunque se usa a menudo la palabra resistencia tanto para el dispositivo como para su propiedad. Su símbolo es una línea quebrada o un rectángulo.

2.1 Asociaciones de resistencias

De manera análoga a los condensadores, los resistores pueden combinarse para formar un circuito con múltiples elementos. Como con los condensadores tenemos dos casos particulares:

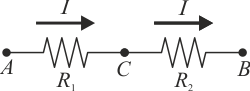
Resistencias en serie: cuando no hay ninguna derivación en el punto de conexión, de manera que toda la corriente que pasa por una pasa por la otra

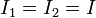
$I_1 = I_2=I\,$

La diferencia de potencial de la asociación es la suma de las individuales. Si A y B son los extremos y C es el punto de conexión

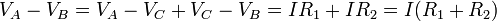
$V_A - V_B = V_A - V_C + V_C - V_B = IR_1+IR_2 = I(R_1+R_2)\,$

por lo que la resistencia equivalente a una asociación en serie de dos resistores es la suma de las resistencias individuales

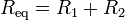
$R_\mathrm{eq}=R_1+R_2\,$

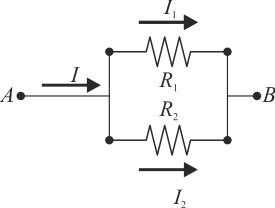
Resistencias en paralelo: cuando se encuentran conectadas por sus dos extremos A y B de forma que la d.d.p. en ambos resistores es la misma

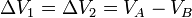
$\Delta V_1 = \Delta V_2 = V_A-V_B\,$

La corriente que llega a la asociación es en este caso la suma de las dos individuales

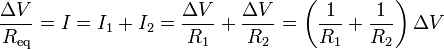
$\frac{\Delta V}{R_\mathrm{eq}}=I= I_1 + I_2 = \frac{\Delta V}{R_1}+\frac{\Delta V}{R_2}=\left(\frac{1}{R_1}+\frac{1}{R_2}\right)\Delta V$

En una asociación en paralelo la conductancia equivalente es la suma de las conductancias individuales

$\frac{1}{R_\mathrm{eq}} = \frac{1}{R_1}+\frac{1}{R_2}\qquad\qquad G_\mathrm{eq}=G_1+G_2$

2.2 Cortocircuito y circuito abierto

Circuito abierto: Un circuito está abierto cuando entre dos puntos se produce una interrupción o se intercala un dieléctrico ideal que impide el paso de corriente. Matemáticamente equivale a decir que entre los puntos se encuentra una conductancia nula (o una resistencia infinita) y por el tramo abierto

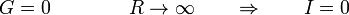
$G=0\qquad\qquad R \to\infty\qquad\Rightarrow\qquad I=0$

Cortocircuito: Un conector ideal en un circuito es un cable que no tiene resistencia eléctrica, $R = 0$ . Esto, por supuesto, constituye una aproximación, pero es razonable si estamos hablando, por ejemplo, de un hilo de cobre con resistencias de miliohmios que conecta dos resistencias de kiloohmios. Gráficamente se representa por una línea simple.

En un conector ideal no hay diferencia de potencial entre sus extremos

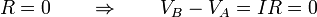
$R=0\qquad\Rightarrow\qquad V_B - V_A = IR = 0\,$

y por tanto todos sus puntos se encuentran al mismo potencial. Desde el punto de vista del circuito equivalente, todos sus puntos son el mismo. Cuando dos elementos están unidos por un conector ideal se dice que están en cortocircuito. Si se coloca un cortocircuito entre dos puntos situados a una cierta diferencia de potencial, el resultado es una corriente de gran intensidad (idealmente infinita), que puede quemar los dispositivos.

3 Amperímetros y voltímetros

3.1 Amperímetros

Un amperímetro (anmeter en inglés) es un dispositivo que mide la intensidad de corriente que circula por una rama de un circuito. Recibe su nombre de la unidad de medida de esta magnitud.

Los principios físicos en los que se basan los amperímetros son variados. Así los hay que miden la desviación en la orientación de una espira en presencia de un campo magnético. También los hay por efecto Hall, que miden la d.d.p. lateral que aparece en un conductor por el que circula una cierta corriente.

En su gran mayoría, los amperímetros se conectan en serie con la rama por la cual circula la corriente que se pretende medir, de forma que ésta lo atraviese.

Si se desea que la lectura del amperímetro corresponda a la corriente que habría si este dispositivo no estuviera presente, es decir, esto obliga a que la resistencia interna de un amperímetro (la que experimenta la corriente al atravesarlo) deba ser pequeña comparada con la del resto de la rama. De no ser así, la corriente se vería reducida y ya la lectura del amperímetro no correspondería a la del circuito sin aparato de medida. En términos de la resistencia de la rama, por estar en serie,

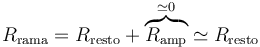
$R_\mathrm{rama}=R_\mathrm{resto}+\overbrace{R_\mathrm{amp}}^{\simeq 0}\simeq R_\mathrm{resto}$

Cuando se trata de medir corriente continua, los amperímetros tienen una polaridad, ya que es preciso asignar un signo a la corriente. Uno de sus terminales se toma como positivo y el otro como negativo (también llamado "común"). Se considera que la intensidad de corriente es positiva si va del polo positivo al común y negativa en caso contrario.

En corriente alterna los amperímetros no tienen polaridad, pues la corriente va sucesivamente en los dos sentidos.

Desde el punto de vista de un análisis de circuito, un amperímetro ideal se comporta como un cortocircuito, es decir, la diferencia de potencial entre sus extremos es nula.

Así, en el circuito de la figura, el amperímetro central conecta la rama superior con la inferior mediante un cortocircuito. De esta manera el sistema puede considerarse formado por una asociación en serie de dos asociaciones en paralelo.

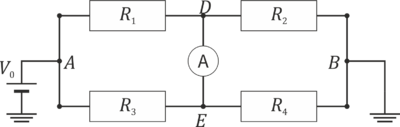
Existen amperímetros de corriente alterna que no van a conectados en serie. Son las "pinzas amperimétricas" que rodean al cable por el que circula la corriente. Estas pinzas se basan en la ley de inducción de Faraday para determinar la corriente que circula.

3.2 Voltímetro

Un voltímetro es un dispositivo que mide la diferencia de potencial o el voltaje entre dos puntos A y B de un circuito. Para ello, el voltímetro se conecta en paralelo con el resto del circuito, estando una terminal conectada en A y la otra en B.

Como con los amperímetros existen diferentes principios en los que basar un voltímetro. En su versión más simple, un voltímetro se puede construir simplemente colocando una resistencia $R 0$ en serie con un amperímetro, de forma que la lectura del amperímetro nos da el voltaje, por simple aplicación de la ley de Ohm

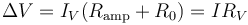
$\Delta V = I_V(R_\mathrm{amp}+R_0) = IR_V\,$

Dado que para que este principio funcione debe haber una corriente que circule por el interior del propio voltímetro, este aparato afecta al resto del circuito (está derivando parte de la corriente). Si se desea que la presencia del voltímetro no afecte al resto del sistema, la resistencia del voltímetro debe ser lo más grande posible (y por tato, la corriente que circula por él, lo menor posible). En términos de la resistencia, por estar en paralelo,

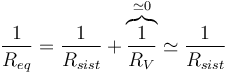
$\frac{1}{R_{eq}}=\frac{1}{R_{sist}}+\overbrace{\frac{1}{R_V}}^{\simeq 0}\simeq \frac{1}{R_{sist}}$

Dicho de otra forma, la lectura del voltímetro sería

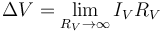
$\Delta V = \lim_{R_V\to\infty}I_VR_V$

En corriente continua, los voltímetros tienen una polaridad, para asignar el signo de la diferencia de potencial. Si el polo positivo del voltímetro está conectado en el punto A y el negativo o común en el punto B, la lectura es $Δ V = V A - V B$ .

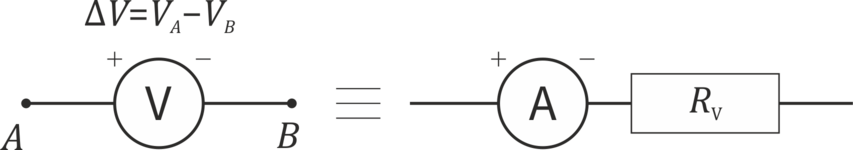
Hay que destacar, porque es importante cuando se estudia la inducción electromagnética, que el voltímetro no funciona "por telepatía", es decir, realmente no mide la diferencia de potencial entre dos puntos del circuito, sino que mide el voltaje a lo largo del propio voltímetro.

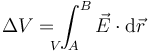
$\Delta V = \int_{\!\!\!\!\!\!\!\!\! V\ A}^B\vec{E}\cdot\mathrm{d}\vec{r}$

En la mayoría de los casos esta lectura coincidirá con el voltaje medido sobre el propio circuito, por la independencia del camino, pero como se ve al estudiar la ley de Faraday esto no siempre es cierto.

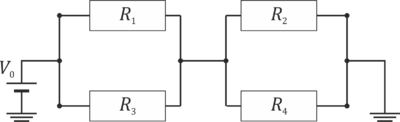
Desde el punto de vista de un análisis de circuito, un voltímetro ideal se comporta como un circuito abierto, es decir, por él no circula corriente.

Así, en el circuito de la figura, el voltímetro central no conecta la rama superior con la inferior y estas pueden suponerse en paralelo.

Nótese la importancia de leer correctamente el circuito, ya que los resultados con un voltímetro son diferentes del mismo circuito con un amperímetro, visto anteriormente.

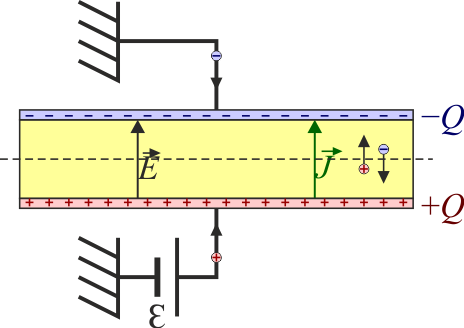
4 Condensador real

Si tenemos un condensador con pérdidas, es decir, el material entre las placas no es un dieléctrico perfecto, sino que permite un cierto flujo de carga por su interior. En este caso, el material vendrá caracterizado por una permitividad $\varepsilon$ y una conductividad $σ$ . En el caso de un condensador plano, la capacidad y la resistencia del elemento pueden calcularse como

$C = \frac{\varepsilon S}{b}\qquad\qquad R=\frac{b}{\sigma S}$

La corriente que llega a este elemento se compone de una parte capacitiva y de una parte resistiva

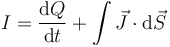
$I = \frac{\mathrm{d}Q}{\mathrm{d}t} +\int \vec{J}\cdot\mathrm{d}\vec{S}$

Archivo:Condensador-real-campos-cargas.png

Ambos términos se pueden poner en función de la diferencia de potencial entre placas

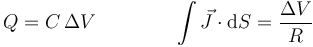
$Q = C\,\Delta V\qquad\qquad \int\vec{J}\cdot\mathrm{d}S=\frac{\Delta V}{R}$

lo que da, para la corriente que llega por el cable

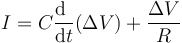
$I = C\frac{\mathrm{d}\ }{\mathrm{d}t}(\Delta V)+\frac{\Delta V}{R}$

Puesto que el resultado da que la corriente que llega al dispositivo es suma de dos términos: corriente capacitiva y corriente resistiva

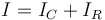
$I=I_C + I_R\,$

por lo que podemos modelarlo como dos elementos en paralelo:

Un condensador ideal, de resistencia infinita (o conductancia cero) por el cual fluye una corriente capacitiva

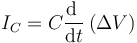
$I_C=C\frac{\mathrm{d}\ }{\mathrm{d}t}\left(\Delta V\right)$

vemos que para que por un condensador ideal fluya una corriente, la tensión debe ser una función variable en el tiempo. En corriente continua un condensador es un circuito abierto y por él no fluye corriente.

Una resistencia ideal, sin capacidad, por la cual fluye la corriente resistiva

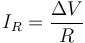
$I_R = \frac{\Delta V}{R}$

Hay que recordar que aunque el circuito equivalente esté formado por dos elementos, en realidad estamos describiendo un solo dispositivo: el condensador real.

En corriente continua solo está la componente resistiva, pero anque no haya componente capacitiva, eso no quiere decir que el condensador esté cargado, solo que su carga no cambia. Podemos preguntarnos cómo es que la carga no cambia si la conductividad del material permiten que las cargas de una placa se vayan a la otra. La explicación es que lo que no cambia es el valor de la carga, pero no las cargas individuales. Cuando un electrón abandona la placa negativa para irse a la positiva, es reemplazado por otro electrón, aportado por la fuente de tensión.

Si se desconecta la fuente de tensión, las cargas que fluyen por el material no son reemplazadas y el condensador se descarga.

Ley de Ohm (GIOI)

De Laplace

Contenido

1 Ley de Ohm

1.1 Aplicación a un conductor filiforme

2 Resistencia eléctrica

2.1 Asociaciones de resistencias

2.2 Cortocircuito y circuito abierto

3 Amperímetros y voltímetros

3.1 Amperímetros

3.2 Voltímetro

4 Condensador real

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES