Modelo de atmósfera isoterma

De Laplace

Revisión a fecha de 21:46 13 mar 2009; Antonio (Discusión | contribuciones)

(dif) ← Revisión anterior | Revisión actual (dif) | Revisión siguiente → (dif)

Contenido

1 Enunciado
2 Solución

1 Enunciado

Suponiendo que la densidad del aire en la atmósfera es proporcional a la presión, demuestre que la variación de la presión atmosférica con la altura es $P (y) = P 0 e - α y$ , siendo $g$ la aceleración de la gravedad y $α = ρ 0 g / P 0$ , con $ρ 0$ y $P 0$ la densidad del aire y la presión atmosférica a nivel del mar ( $y = 0$ ).

2 Solución

2.1 Introducción

Antes de resolver el problema, es conveniente aclarar la razón de la palabra "isoterma" del título. Puede parecer incongruente, dado que en el enunciado del problema no se hace mención alguna a la temperatura.

La causa es la hipótesis “Suponiendo que la densidad del aire en la atmósfera es proporcional a la presión”.

¿Por qué es razonable hacer esta hipótesis? Para entenderlo, observamos que el aire se comporta aproximadamente como un gas ideal. Para un gas ideal, se cumple la ecuación de estado

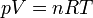
$pV = n R T\,$

$R$ es la constante de los gases ideales y la cantidad $n$ es el número de moles, que será igual a la masa total del gas que tengamos, dividida por su peso molecular, esto es

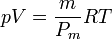
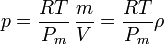
$p V = \frac{m}{P_m}RT$ $\Rightarrow$ $p = \frac{RT}{P_m}\,\frac{m}{V}=\frac{RT}{P_m}\rho$

Si la temperatura del gas es la misma en todos los puntos, la presión es proporcional a la densidad, pero si varía, habrá que tenerlo en cuenta. La hipótesis de partida habrá dejado de ser cierta.

Para evitar usar el peso molecular, que para el aire es simplemente un promedio (pues se trata de una mezcla de gases), podemos escribir la ecuación anterior como

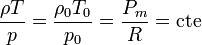
$\frac{\rho T}{p}= \frac{\rho_0 T_0}{p_0}=\frac{P_m}{R}=\mathrm{cte}$

siendo $p 0$ , $ρ 0$ y $T 0$ la presión densidad y temperatura en un punto concreto, por ejemplo, al nivel del mar. De aquí

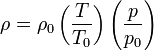
$\rho = \rho_0\left(\frac{T}{T_0}\right)\left(\frac{p}{p_0}\right)$

si la temperatura es la misma en todos los puntos

$\rho = \frac{\rho_0}{p_0}p$

Esta es la hipótesis que haremos en el siguiente apartado. Más adelante veremos como queda si suponemos una temperatura que varía con la altura.

2.2 Solución isoterma

Consideremos una capa de aire de pequeño espesor $d z$ y sección transversal $S$ situada a una altura $z$ . Puesto que esta capa se encuentra en equilibrio, la suma de fuerzas sobre ella es igual a 0.

Las fuerzas que actúan sobre esta lámina son su peso y la debidas a la presión en sus caras superior e inferior.

El peso de la lámina es igual a la aceleración de la gravedad multiplicada por la masa de la lámina, a su vez igual a la densidad por el volumen:

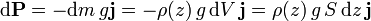
$\mathrm{d}\mathbf{P}= -\mathrm{d}m\,g\mathbf{j}=-\rho(z)\,g\,\mathrm{d}V\,\mathbf{j}=\rho(z)\,g\,S\,\mathrm{d}z\,\mathbf{j}$

La fuerza debida a la presión ejercida por el aire situado debajo de la capa será igual a la presión a esa altura multiplicada por la sección transversal, e irá dirigida hacia arriba

No se pudo entender (Falta el ejecutable de texvc. Por favor, lea math/README para configurarlo.): \mathbf{F}_{\mathrm{inf}=p(z)\,S\,\mathbf{j}

La fuerza debida a la presión ejercida por el aire situado arriba irá dirigida hacia abajo y valdrá, análogamente

No se pudo entender (Falta el ejecutable de texvc. Por favor, lea math/README para configurarlo.): \mathbf{F}_{\mathrm{sup}=-p(z+\mathrm{d}z)\,S\,\mathbf{j}

La condición de equilibrio nos da

$\mathbf{0}=\sum\mathbf{F}=\left(-\rho(z)\,g\,\mathrm{d}z+p(z)-p(z+\mathrm{d}z)\right)\,S\,\mathbf{j}$

Podemos reescribir esta condición como

No se pudo entender (Falta el ejecutable de texvc. Por favor, lea math/README para configurarlo.): \frac{p(z+\mathrm{d}z)-p(z)}{\mathrm{d}z)=-\rho(z)g

El primer miembro de esta ecuación es, por definición, la derivada de la presión con respecto a la altura $z$ , lo que nos da la ecuación diferencial

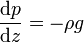
$\frac{\mathrm{d}p}{\mathrm{d}z}=-\rho g$

Esta ecuación es válida para cualquier variación de la densidad (siempre que se cumpla la condición de que la atmósfera se encuentra en equilibrio.

Sustituyendo ahora la relación de proporcionalidad entre la densidad y la presión, válida para la atmósfera isoterma

$\frac{\mathrm{d}p}{\mathrm{d}z}=-\frac{\rho_0g}{p_0}p$

Se trata de hallar ahora una función cuya derivada es proporcional a la propia función. Esta es una propiedad característica de las exponenciales. Supongamos que la presión es de la forma

p = p 0 e k z

2.3 Solución para un perfil de temperaturas

Modelo de atmósfera isoterma

De Laplace

Contenido

1 Enunciado

2 Solución

2.1 Introducción

2.2 Solución isoterma

2.3 Solución para un perfil de temperaturas

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES