Campo de un plano infinito (GIOI)
De Laplace
1 Enunciado
Empleando el resultado del problema “Campo de un disco homogéneo”, halle el campo eléctrico en cualquier punto del espacio debido a un plano infinito cargado uniformemente con una densidad de carga σ0.
2 Solución
Al hallar el campo en el eje de un disco se llega a que su valor es
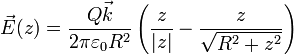
En términos de la densidad de carga superficial
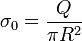
este campo se expresa
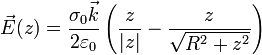
Para obtener el campo debido a un plano infinito con una densidad de carga uniforme, simplemente consideramos el límite de un disco cuyo radio tiende a infinito
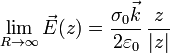
Si separamos en los dos semiespacios, teniendo en cuenta que
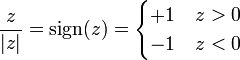
queda
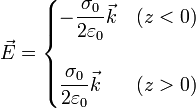
En principio, este resultado solo vale para el eje del disco. Sin embargo, cuando éste se extiende a todo un plano, cualquier recta normal al plano puede considerarse como eje de un disco cuyo límite es el plano. Por tanto, el resultado anterior es válido para todos los puntos del espacio.
Por supuesto, los planos infinitos no existen en la realidad, pero el resultado anterior sirve como aproximación al campo creado por una superficie plana cargada, siempre que no estemos muy alejada de ella (y la veamos por tanto como “infinita”).
Este resultado nos dice que, a diferencia de lo que ocurre para una carga puntual, el campo creado por un plano infinito uniformemente cargado es independiente de la distancia al plano. No disminuye al alejarnos de él. El cómo es posible que sumando campos que disminuyen con la distancia resulte un campo que no lo hace, puede entenderse notando que al alejarnos del plano, el campo de cada carga disminuye, pero a cambio “vemos” el campo de más cargas y un factor se cancela con el otro.
