Problemas de electrostática en el vacío (GIOI)

De Laplace

Revisión a fecha de 13:55 13 feb 2020; Antonio (Discusión | contribuciones)

(dif) ← Revisión anterior | Revisión actual (dif) | Revisión siguiente → (dif)

1 Carga total de una distribución

Calcule la carga total de las siguientes distribuciones de carga:

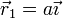N cargas de valor q situadas en los vértices de un polígono regular de N lados situado en el plano XY, con centro el origen y cuyo primer vértice se encuentra en $\vec{r}_1=a\vec{\imath}$ .
Un anillo circular de radio R con una densidad lineal de carga uniforme $λ 0$ .
Un anillo circular de radio R con centro el origen y situado en el plano XY, con una densidad lineal de carga $λ(θ) = λ 0 cos(θ)$ , siendo θ el ángulo del vector de posición con el eje OX.
Una superficie esférica de radio a con una densidad de carga uniforme $σ 0$ , rodeada por una superficie esférica concéntrica de radio b con densidad de carga $- σ 0$ .
Una esfera maciza de radio R con densidad de carga uniforme $ρ 0$ .
Una esfera maciza de radio $2 R$ con una densidad de carga dependiente de la distancia al centro como $ρ(r) = A (R - r)$ ( $r < 2 R$ ).

2 Cargas en un triángulo equilátero

Tres cargas puntuales iguales +q se hallan en los vértices de un triángulo equilátero de lado b. Calcule la fuerza eléctrica sobre cada una de ellas. Suponga que se cambia una de las cargas +q por una carga –q. ¿Cuánto vale en ese caso la fuerza sobre cada una de las tres cargas? Si se cambia una segunda carga +q por otra carga –q, ¿cuánto pasa a ser la fuerza sobre cada una? Por último, si se sustituye la última carga +q por otra –q, ¿cuál es ahora la fuerza? Solución

3 Fuerzas y momentos sobre un par de cargas

Dos cargas $q 1 = + q$ y $q 2 = - q$ se encuentran en los extremos de una varilla que se encuentra inmersa en el campo eléctrico

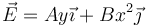
$\vec{E}=Ay\vec{\imath}+Bx^2 \vec{\jmath}$

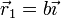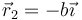Si los extremos de la varilla se encuentran en $\vec{r}_1=b\vec{\imath}$ y $\vec{r}_2=-b\vec{\imath}$ , ¿cuál es el efecto del campo sobre el sistema?
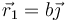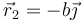Si los extremos de la varilla se encuentran en $\vec{r}_1=b\vec{\jmath}$ y $\vec{r}_2=-b\vec{\jmath}$ , ¿cuál es el efecto del campo sobre el sistema?