Péndulo compuesto
De Laplace
Contenido |
1 Enunciado
Se tiene un péndulo compuesto consistente en una barra de longitud b y masa M suspendida por un punto situado a una distancia d del centro de la barra (d < b / 2). Suponiendo que la barra se desvía un ángulo pequeño θ0 respecto de la vertical y a partir de ahí se suelta:
- Determine el periodo de oscilación de la barra
- Suponga ahora que la barra se sitúa horizontalmente y desde ahí se suelta. Para el instante en que pasa por la vertical, calcule:
- La velocidad angular de la barra y la velocidad lineal de los extremos de la barra.
- Calcule la fuerza ejercida sobre el punto de anclaje.
- Calcule la tensión en cada punto de la barra.
2 Periodo
Determinaremos en primer lugar la ecuación de movimiento para el ángulo θ que la barra forma con la vertical. Esto se puede hacer a partir de las fuerzas aplicadas o mediante la ley de conservación de la energía mecánica.
2.1 Analizando las fuerzas aplicadas
También puede resolverse el problema aplicando el teorema de la cantidad de movimiento y el del momento cinético.
La barra constituye un sólido rígido sometido a dos fuerzas:
- Su peso,
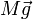
- La fuerza de reacción,
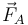 ejercida por el soporte en el punto de anclaje A.
ejercida por el soporte en el punto de anclaje A.
No hay ningún momento de reacción ya que en el punto de anclaje la barra puede girar libremente.
La suma de estas dos fuerzas produce la aceleración del centro de masas
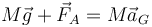
En esta ecuación, la fuerza de reacción es también una incógnita (no sabemos ni su módulo ni su dirección y sentido), por lo que esta ecuación no nos basta para determinar el movimiento del CM.
Para aplicar el teorema del momento cinético podemos considerar el centro de masas o un punto fijo. La máxima simplificación la conseguimos reduciendo en el punto de anclaje A, ya que el momento de la fuerza de reacción respecto a este punto es nulo y por tanto desaparece de la ecuación.
Queda entonces

siendo el momento cinético respecto a este punto
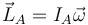
El momento de inercia que aparece en esta ecuación es el correspondiente al punto A, el cual se calcula por el teorema de Steiner

Puede hallarse también sin usar el teorema de Steiner empleando la descomposición
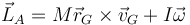
y sustituyendo la posición y velocidad del CM, que describe un arco de circunferencia.
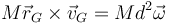
Hemos elegido un sistema de ejes centrado en el soporte con OX el horizontal en el plano del péndulo y OY el vertical (OZ sería perpendicular a ambos e iría hacia el exterior de la figura).
El momento de las fuerzas respecto al punto A es
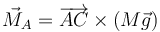
Aquí no aparece el momento de la fuerza de reacción porque estamos calculándolo justo en su punto de aplicación. La recta soporte del peso pasa a una distancia
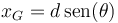
del punto de anclaje produciendo un giro en sentido negativo, por lo que
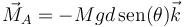
Queda entonces la ecuación

lo que nos da la ecuación del péndulo
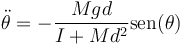
Si el ángulo de desviación es pequeño puede aproximarse el seno por su argumento y escribirse
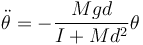
que es la ecuación de un oscilador armónico de frecuencia angular
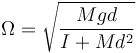
a la cual corresponde un periodo
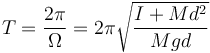
Sustituyendo el valor del momento de inercia queda
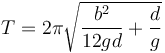
Vemos que el periodo es independiente de la masa de la barra, resultado conocido por análisis dimensional del problema.
El periodo sí depende de dónde se encuentra el soporte a lo largo de la barra.
Si se encuentra en el extremo d = b / 2 y este periodo vale
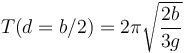
Este periodo es aproximadamente un 20% más corto que el del péndulo simple se la misma longitud y la misma masa.
Cuando el soporte se va situando cada vez más cerca del centro (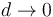 ) el periodo va creciendo de forma ilimitada, tendiendo a infinito para un soporte justo en el centro. Esto ocurre porque justo en esa posición el peso no provoca par alguno sobre el péndulo y no lo hace oscilar. La barra se queda en equilibrio en cualquier orientación respecto a la vertical (o bien gira uniformemente).
) el periodo va creciendo de forma ilimitada, tendiendo a infinito para un soporte justo en el centro. Esto ocurre porque justo en esa posición el peso no provoca par alguno sobre el péndulo y no lo hace oscilar. La barra se queda en equilibrio en cualquier orientación respecto a la vertical (o bien gira uniformemente).
2.2 Aplicando la ley de conservación de la energía
De acuerdo con el teorema de las fuerzas vivas para un sólido (o teorema trabajo-energía cinética), se cumple
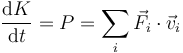
- Su peso,
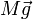 , aplicado en el CM
, aplicado en el CM
- La fuerza de reacción,
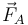 ejercida por el soporte y aplicada en la posición de éste, que es fija.
ejercida por el soporte y aplicada en la posición de éste, que es fija.
De estas dos, solo el peso desarrolla una potencia, ya que la velocidad del punto de anclaje es nula.
A su vez, por tratarse de una fuerza conservativa, la potencia del peso es igual al ritmo de disminución de la energía potencial
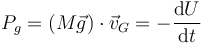
siendo U la energía potencial gravitatoria
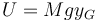
Por tanto, al ser la potencia debida a una fuerza conservativa, la energía mecánica se conserva

- Energía cinética
- la energía cinética la podemos descomponer en parte de traslación, KT y parte de rotación, KR. El CM describe un arco circular alrededor del punto de anclaje, a una distancia d de este. Si θ es el ángulo que la barra forma con la vertical
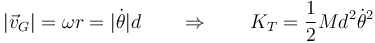
- La de rotación vale

- La total es suma de estas dos
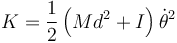
- Vemos que podemos calcular esta energía cinética directamente como la de una rotación en torno al punto fijo A, usando el teorema de Steiner para hallar el momento de inercia correspondiente.
- Energía potencial
- Si llamamos y a la coordenada vertical, con y = 0 la altura del punto de anclaje, podemos escribir la energía potencial como
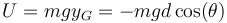
- el signo negativo proviene de que por debajo de A la coordenada y es negativa pero el coseno es positivo.
Sumando las dos contribuciones
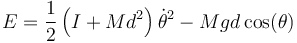
Obtenemos la ecuación de movimiento derivando esta ecuación respecto al tiempo, aplicando que
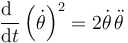
y
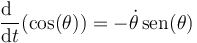
Por tanto
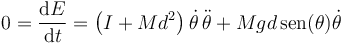
Despejamos de aquí la aceleración angular
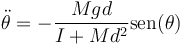
Esta es la ecuación del péndulo compuesto, que no tiene por qué ser una barra. En el caso particular de la barra queda
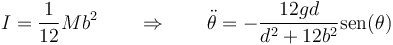
Si además la barra está sujeta por su extremo d = b / 2 y

En general, el periodo de oscilación de un péndulo depende de la amplitud, pero si el ángulo de desviación es pequeño
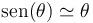
y queda la ecuación de un oscilador armónico
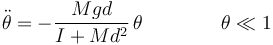
siendo la frecuencia de oscilación
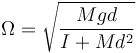
y el periodo
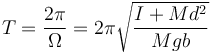
que para el caso de la barra se reduce a
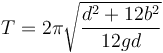
y si está sujeta por su extremo
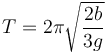
3 Paso por la vertical
3.1 Velocidades
La velocidad que tiene la varilla en su paso por la vertical se puede calcular empleando la conservación de la energía mecánica.
Si la barra está inicialmente en reposo en la posición horizontal, tanto la energía cinética como la potencial son nulas.
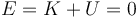
Cuando la barra pasa por la posición vertical parte de su energía cinética se habrá convertido en energía potencial, pero su suma debe seguir siendo la misma, de manera que
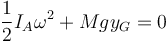
siendo

Esto nos da
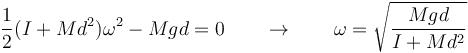
La velocidad lineal de cada extremo la da la ecuación para una rotación alrededor de un punto fijo. Para el extremo inferior
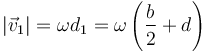
y para el superior
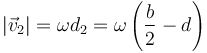
siendo ambas horizontales, pero de sentido contrario.
3.2 Fuerza de reacción
Una vez que tenemos el movimiento del péndulo podemos hallar la fuerza de reacción a partir de la ecuación para la cantidad de movimiento
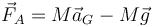
Cuando el péndulo pasa por su punto más bajo, el peso y la aceleración del CM son verticales, con lo que la fuerza de reacción también lo será.
El CM de la barra describe un arco de circunferencia de radio d alrededor del soporte. En el punto más bajo su rapidez es máxima, con lo que la aceleración tangencial es nula y su aceleración es puramente normal
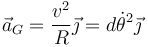
Sustituimos aquí la velocidad angular calculada antes
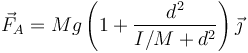
En el caso particular de una barra sujeta por su extremo, esto se reduce a






