Péndulo simple (CMR)

De Laplace

1 Enunciado

Un péndulo simple está formado por una masa m unida a una varilla rígida de longitud 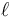, unida por su otro extremo a un punto fijo O mediante una articulación esférica. La masa está sometida a la acción del peso.

1. Considere, en primer lugar, el movimiento en un plano vertical. Determine la ecuación de movimiento para el ángulo θ que la varilla forma con la vertical. ¿Qué puntos de equilibrio existen? ¿Son estables o inestables?
2. Considere el caso de un péndulo cónico, el cual gira con velocidad angular constante 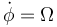alrededor del eje vertical. ¿Cuál debe ser la relación entre Ω y el ángulo con la vertical, θ, para que este movimiento sea posible? ¿Puede conseguirse un movimiento circular sea cual sea Ω?
3. Suponga ahora el movimiento general, en el cual puede cambiar tanto θ como el ángulo , de giro alrededor del eje vertical. A partir de la 2ª ley de Newton, obtenga las ecuaciones de movimiento para estos dos ángulos. Esto puede hacerse de diferentes maneras:
   1. Empleando coordenadas esféricas.
   2. Empleando un sistema de referencia en rotación alrededor del eje vertical, y empleando las fuerzas ficticias necesarias.
   3. Considerando una composición de movimientos mediante tres sistemas de referencia: uno fijo “1”, uno intermedio “2” que gira alrededor del eje vertical un ángulo φ y uno ligado “3” que gira respecto a un eje horizontal un ángulo θ.
4. Considerando el caso general, con movimiento en las dos coordenadas y θ, suponga que con un motor se fuerza a una rotación constante 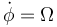. En ese caso, ¿cómo queda la ecuación para θ? ¿Qué puntos de equilibrio hay? ¿Son estables o inestables?

2 Movimiento plano

3 Movimiento cónico

4 Caso general

5 Rotación forzada

6 Deducción alternativa del caso general

6.1 Empleando tres sistemas de referencia

6.2 Empleando coordenadas esféricas