Curvas y peraltes (GIOI)

De Laplace

Revisión a fecha de 18:02 1 ene 2006; Antonio (Discusión | contribuciones)

(dif) ← Revisión anterior | Revisión actual (dif) | Revisión siguiente → (dif)

Contenido

1 Enunciado
2 Caso sin rozamiento
3 Caso con rozamiento
- 3.1 Velocidad mínima
- 3.2 Velocidad máxima
4 Valores numéricos

1 Enunciado

El circuito de Indianapolis posee curvas de 200 m de radio peraltadas un ángulo de 9°12'. Si no se considera el rozamiento, ¿con qué rapidez debe ir un coche si no quiere deslizarse ni hacia arriba ni hacia abajo? El coeficiente de rozamiento lateral de un coche con la pista vale μ = 1.50. ¿Cuáles son las velocidades máximas y mínimas que puede adquirir un coche sin derrapar?

2 Caso sin rozamiento

El caso sin rozamiento es idéntico al del péndulo cónico formado por una Masa sujeta de un hilo. Allí actúan dos fuerzas: el peso, vertical hacia abajo, y la tensión, radial hacia el punto de sujeción. En el caso del peralte también actúa el peso y en lugar de la tensión tenemos la reacción normal del suelo. En ambos casos, la accón conjunta de ambas fuerzas produce una aceleración normal horizontal, que genera un movimiento circular uniforme horizontal.

Por ello, el análisis del caso del peralte sin rozamiento puede realizarse exactamente de la misma manera que en ese problema.

No obstante, aquí emplearemos un planteamiento ligeramente diferente, que conduce al mismo resultado y se generaliza al caso con rozamiento.

Tenemos un plano inclinado un ángulo β de forma que el vehículo se encuentra sobre él. Su movimiento no es a lo largo del plano, hacia arriba o hacia abajo, sino perpendicular a él.

A la hora de elegir los ejes de coordenadas tenemos dos elecciones posibles:

Un sistema $O X 1 Y 1$ en el que el vector 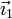$\vec{\imath}_1$ es horizontal y el vector 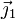$\vec{\jmath}_1$ es vertical (en la dirección del peso)
Un sistema $O X 2 Y 2$ en el que el vector 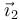$\vec{\imath}_2$ es tangente al plano, cuesta arriba, y el vector 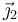$\vec{\jmath}_2$ es normal al plano.

La relación entre estas dos bases es:

$\begin{array}{rclcrcl} \vec{\imath}_2&=&C \vec{\imath}_1+S\vec{\jmath}_1 &\qquad\qquad & \vec{\imath}_1&=&C \vec{\imath}_2-S\vec{\jmath}_2 \\ \vec{\jmath}_2&=&-S\vec{\jmath}_1+C\vec{\jmath}_2 &\qquad\qquad & \vec{\jmath}_1&=&S \vec{\imath}_2+C\vec{\jmath}_2 \end{array}$

donde usamos las abreviaturas

$C=\cos(\theta)\qquad\qquad S=\mathrm{sen}(\beta)$

Ambos sistemas tienen sus ventajas y sus inconvenientes: el primero es más adecuado para representar el peso y la aceleración normal (que es horizontal), mientras que el segundo es preferible para escribir la reacción normal y la fuerza de rozamiento.

Podemos, por supuesto, emplear uno solo de los dos sistemas y descomponer cada fuerza en los ejes elegidos. No obstante, no estamos obligados a hacerlo desde el principio. Podemos emplear ambas bases al mismo tiempo, siempre que tengamos cuidado en distinguirlas.

Para resolver el problema, aplicamos la segunda ley de Newton. En el caso sin rozamiento, queda

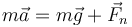
$m\vec{a}=m\vec{g}+\vec{F}_n$

Escribimos cada vector en función de las bases y teniendo en cuenta que la aceleración normal es horizontal, queda

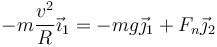
$-m\frac{v^2}{R}\vec{\imath}_1 = -mg\vec{\jmath}_1+F_n\vec{\jmath}_2$

Aquí v es la rapidez del vehículo y R es el radio de la circunferencia que describe.

Podemos sustituir una de las bases en función de la otra e igualar componente a componente, pero es más rápido eliminar la fuerza normal, que es desconocida, proyectando en una dirección ortogonal a ella. Es decir, multiplicamos escalarmente por 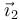$\vec{\imath}_2$

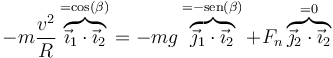
$-m\frac{v^2}{R}\overbrace{\vec{\imath}_1\cdot\vec{\imath}_2}^{=\cos(\beta)} = -mg\overbrace{\vec{\jmath}_1\cdot\vec{\imath}_2}^{=-\mathrm{sen}(\beta)}+F_n\overbrace{\vec{\jmath}_2\cdot\vec{\imath}_2}^{=0}$

y nos queda

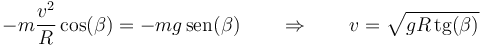
$-m\frac{v^2}{R}\cos(\beta)=-mg\,\mathrm{sen}(\beta) \qquad\Rightarrow\qquad v=\sqrt{gR\,\mathrm{tg}(\beta)}$

Esta es la única velocidad a la que puede circular el vehículo si no desliza hacia abajo ni hacia arriba. Si va más lento, domina la gravedad, R disminuye y el vehículo se va hacia abajo. Si va más rápido, R aumenta y se va hacia arriba.

3 Caso con rozamiento

El rozamiento de las ruedas con el suelo permite un mayor rango de velocidades. Si la velocidad baja, impide que deslice hacia abajo del plano y si sube, impide que derrape hacia arriba. Este rozamiento es estático, por lo que debe cumplir

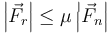
$\left|\vec{F}_r\right|\leq \mu \left|\vec{F}_n\right|$

Esta fuerza de rozamiento es tangente a la superficie, por lo que la segunda ley de Newton se escribe ahora

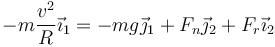
$-m\frac{v^2}{R}\vec{\imath}_1 = -mg\vec{\jmath}_1+F_n\vec{\jmath}_2+F_r\vec{\imath}_2$

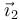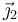Aquí $F r$ puede ser tanto posiivo (hacia arriba, para velocidades bajas) como negativo (hacia abajo, para velocidades altas). Multiplicando escalarmente por $\vec{\imath}_2$ y por $\vec{\jmath}_2$ , como antes, resultan las ecuaciones

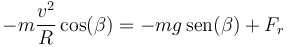
$-m\frac{v^2}{R}\cos(\beta)=-mg\,\mathrm{sen}(\beta) +F_r$

{}

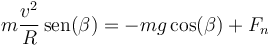
$m\frac{v^2}{R}\,\mathrm{sen}(\beta)=-mg\cos(\beta) +F_n$

De donde

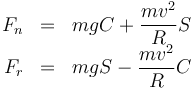
$\begin{array}{rcl}F_n&=&mgC+\dfrac{mv^2}{R}S \\ F_r&=&mgS-\dfrac{mv^2}{R}C \end{array}$

Para hallar la velocidad mínima y la máxima admisibles, consideramos los casos de deslizamiento inminente, es decir, aquellos en que la fuerza de rozamiento tiene el máximo módulo posible.

3.1 Velocidad mínima

La velocidad mínima se alcanza cuando la fuerza de rozamiento es hacia arriba y vale $μ F n$ , es decir,

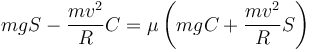
$mgS-\dfrac{mv^2}{R}C = \mu \left(mgC+\dfrac{mv^2}{R}S\right)$

Despejamos la velocidad y da

$v_\mathrm{min}=\sqrt{gR\frac{S-\mu C}{C+\mu S}}$

Podemos ver que en el caso sin rozamiento se reduce al valor calculado en la sección anterior.

3.2 Velocidad máxima

La velocidad máxima se alcanza cuando la fuerza de rozamiento es hacia abajo y vale $- μ F n$ , es decir,

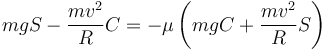
$mgS-\dfrac{mv^2}{R}C = -\mu \left(mgC+\dfrac{mv^2}{R}S\right)$

Despejamos la velocidad y da

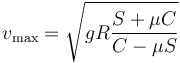
$v_\mathrm{max}=\sqrt{gR\frac{S+\mu C}{C-\mu S}}$

(basta cambiar μ por −μ)

En el caso sin rozamiento también se reduce al valor calculado en la sección anterior.

4 Valores numéricos

Para el caso en que

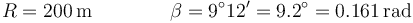
$R=200\,\mathrm{m} \qquad\qquad \beta=9^\circ 12'=9.2^\circ = 0.161\,\mathrm{rad}$

tenemos que

$C=cos(\beta)=0.9872\qquad\qquad S=\,\mathrm{sen}(\beta)=0.1599$

lo que nos da la velocidad, para el caso sin rozamiento

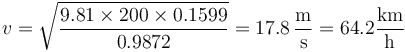
$v=\sqrt{\dfrac{9.81\times 200\times 0.1599}{0.9872}}=17.8\,\frac{\mathrm{m}}{\mathrm{s}}=64.2\frac{\mathrm{km}}{\mathrm{h}}$

El valor máximo, con el rozamiento μ = 1.5 es

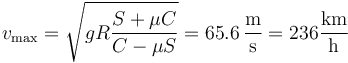
$v_\mathrm{max}=\sqrt{gR\frac{S+\mu C}{C-\mu S}}=65.6\,\frac{\mathrm{m}}{\mathrm{s}}=236\frac{\mathrm{km}}{\mathrm{h}}$

mientras que la mínima la da

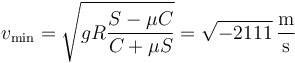
$v_\mathrm{min}=\sqrt{gR\frac{S-\mu C}{C+\mu S}}=\sqrt{-2111}\,\frac{\mathrm{m}}{\mathrm{s}}$

El que resulte la raíz cuadrada de un número negativo, es decir, una velocidad imaginaria, lo que nos dice es que en realidad la velocidad mínima es 0. El rozamiento estático es suficiente para matener el coche en su posición incluso aunque quede parado en la pista.

Esto es lo habitual. La utilidad del peralte es permitir velocidades más altas. Para la misma curva sin peraltar (β = 0) la velocidad límite sería

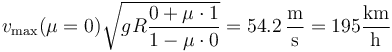
$v_\mathrm{max}(\mu=0)\sqrt{gR\frac{0+\mu\cdot 1}{1-\mu \cdot 0}}=54.2\,\frac{\mathrm{m}}{\mathrm{s}}=195\frac{\mathrm{km}}{\mathrm{h}}$

Por encima de esta velocidad, el coche derraparía.

Curvas y peraltes (GIOI)

De Laplace

Contenido

1 Enunciado

2 Caso sin rozamiento

3 Caso con rozamiento

3.1 Velocidad mínima

3.2 Velocidad máxima

4 Valores numéricos

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES