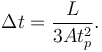De Laplace

Revisión a fecha de 11:41 8 nov 2019; Pedro (Discusión | contribuciones)

(dif) ← Revisión anterior | Revisión actual (dif) | Revisión siguiente → (dif)

Contenido

1 Enunciado
2 Solución
- 2.1 Tensión en la cuerda
- 2.2 Movimiento con
  - 2.2.1 Parada súbita de la masa 2

1 Enunciado

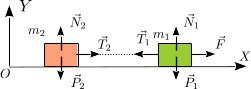
Las masas puntuales $m 1$ y $m 2$ se deslizan sin rozamiento sobre una superficie horizontal. Las masas están unidas por una cuerda ideal, inextensible y sin masa, de longitud $L$ . Una fuerza 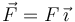$\vec{F}=F\,\vec{\imath}$ actúa sobre la masa $m 1$ . Las masas se mueven de modo que la cuerda está siempre tensa.

Calcula la tensión de la cuerda durante el movimiento
Supongamos ahora que las dos masas son iguales, m₁ = m₂ = m₀. En el instante inicial la masa m₂ esta en el punto O y la cuerda está completamente estirada. Las dos masas están en reposo en este instante inicial. Ahora la fuerza depende del tiempo como , siendo A una constante.
1. Cuáles son las unidades base de $A$ en el S.I.
2. ¿Cuál es la posición de la masa $m 1$ en función del tiempo?
3. En el instante $t = t p$ la partícula 1 se para súbitamente. ¿Cuanto tiempo tarda en chocar con ella la partícula 2?

2 Solución

2.1 Tensión en la cuerda

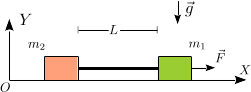
La figura de la derecha muestra las fuerzas que actúan sobre cada masa. Tenemos que aplicar la Segunda Ley de Newton a cada masa por separado

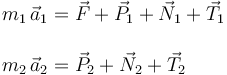
$\begin{array}{l} m_1\,\vec{a}_1 = \vec{F} + \vec{P}_1 + \vec{N}_1 + \vec{T}_1\\ \\ m_2\,\vec{a}_2 = \vec{P}_2 + \vec{N}_2 + \vec{T}_2 \end{array}$

Expresamos los vectores que aparecen aquí en el sistema de ejes de la figura. Para la masa 1 tenemos

$\begin{array}{l} \vec{a}_1 = a\,\vec{\imath},\\ \vec{F} = F\,\vec{\imath},\\ \vec{P}_1 = -m_1g\,\vec{\jmath},\\ \vec{N}_1 = N_1\,\vec{\jmath},\\ \vec{T}_1 = -T\,\vec{\imath},\\ \end{array}$

Para la masa 2 tenemos

$\begin{array}{l} \vec{a}_2 = a\,\vec{\imath},\\ \vec{P}_2 = -m_2g\,\vec{\jmath},\\ \vec{N}_2 = N_2\,\vec{\jmath},\\ \vec{T}_2 = T\,\vec{\imath},\\ \end{array}$

Hemos usado que la aceleración de las dos masas debe ser la misma y que la tensión de la cuerda es la misma en todos sus puntos, pues no tiene masa. A partir de las expresiones vectoriales de la Segunda Ley de Newton obtenemos cuatro ecuaciones escalares

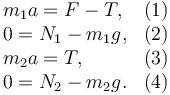
$\begin{array}{lr} m_1a = F - T, & (1)\\ 0 = N_1-m_1g, & (2)\\ m_2a = T, & (3)\\ 0 = N_2 - m_2g. & (4) \end{array}$

Sumando las ecuaciones (1) y (3) obtenemos la aceleración de la masa

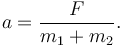
$a = \dfrac{F}{m_1+m_2}.$

A partir de (3) obtenemos la tensión en la cuerda

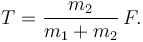
$T = \dfrac{m_2}{m_1+m_2}\,F.$

Las ecuaciones (2) y (4) nos dan las magnitudes de las fuerzas normales

$N_1 = m_1g, \qquad N_2 = m_2g.$

2.2 Movimiento con $\mathbf{F = 12m_0At}$

Durante el movimiento la distancia entre las masas es constante. Entonces, las dos tienen la misma velocidad y aceleración.

Las unidades base de $A$ deben ser tales que la definición de $F$ sea compatible con las unidades de fuerza

$[A] = \dfrac{[F]}{[m_0][t]} = \mathrm{\dfrac{N}{kg\cdot s} = \dfrac{kg\cdot m\cdot s^{-2}}{kg\cdot s} = \dfrac{m}{s^3}}.$

Introducimos la definición de $F$ en la expresión que nos da la aceleración d elas masas

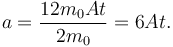
$a = \dfrac{12m_0At}{2m_0} = 6At.$

Esta aceleración depende del tiempo. Para obtener la velocidad hay que resolver la ecuación diferencial

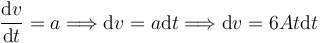
$\dfrac{\mathrm{d}v}{\mathrm{d}t} = a \Longrightarrow \mathrm{d}v = a\mathrm{d}t \Longrightarrow \mathrm{d}v = 6At\mathrm{d}t$

Integrando obtenemos

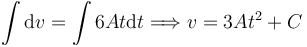
$\int\mathrm{d}v = \int 6At\mathrm{d}t \Longrightarrow v = 3At^2 + C$

En el instante inicial las masas estaban en reposo. Por tanto

$v(0) = 0 \Longrightarrow C = 0.$

Es decir, la velocidad de las masas en función del tiempo es

$v 1 = v 2 = 3 A t 2 .$

Para obtener la coordenada $x$ de cada masa debemos resolver la ecuación diferencial correspondiente. Para la masa $m 1$ tenemos

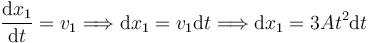
$\dfrac{\mathrm{d}x_1}{\mathrm{d}t} = v_1 \Longrightarrow \mathrm{d}x_1 = v_1\mathrm{d}t \Longrightarrow \mathrm{d}x_1 = 3At^2\mathrm{d}t$

Integrando obtenemos

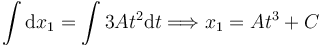
$\int\mathrm{d}x_1 = \int 3At^2\mathrm{d}t \Longrightarrow x_1 = At^3 + C$

En el instante inicial la cuerda estaba estirada. Por tanto

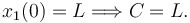
$x_1(0) = L \Longrightarrow C = L.$

Es decir

$x 1 = L + A t 3 .$

Procediendo de manera similar para la masa $m 2$ obtenemos

$x 2 = A t 3 .$

2.2.1 Parada súbita de la masa 2

En $t = t p$ la masa $m 1$ se para. En ese instante, la cuerda deja de tirar de la masa $m 2$ . Por tanto, la aceleración de $m 2$ es cero a partir de ese instante y se mueve con velocidad constante e igual a la que tenía en $t p$

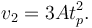
$v_2 = 3At_p^2.$

En $t = t p$ la distancia entre las masas era $L$ . Como la masa 2 se mueve con velocidad uniforme, el tiempo que tarda en chocar con la otra masa es el que tarda en recorrer esa distancia

$\Delta t = \dfrac{L}{3At_p^2}.$

Masas con cuerda horizontal (Oct. 2019 G.I.C.)

De Laplace

Contenido

1 Enunciado

2 Solución

2.1 Tensión en la cuerda

2.2 Movimiento con $\mathbf{F = 12m_0At}$

2.2.1 Parada súbita de la masa 2

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES