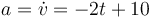Velocidad dependiente del tiempo (GIOI)

De Laplace

Revisión a fecha de 15:22 2 oct 2019; Antonio (Discusión | contribuciones)

(dif) ← Revisión anterior | Revisión actual (dif) | Revisión siguiente → (dif)

Contenido

1 Enunciado
2 Desplazamiento neto
3 Gráfica de la aceleración
4 Frenado de la partícula
5 Rapidez media

1 Enunciado

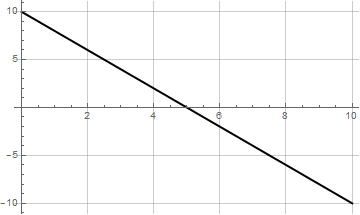
Una partícula describe un movimiento rectilíneo cuya velocidad, como función del tiempo entre $t=0\,\mathrm{s}$ y $t=10\,\mathrm{s}$ es la parábola de la figura.

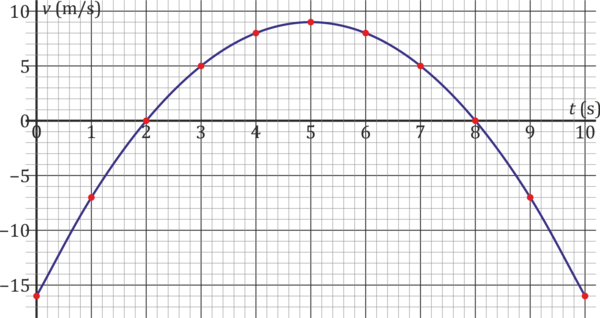
¿Cuánto vale, aproximadamente, el desplazamiento neto en el intervalo [0s, 10s]?
¿Cómo es la gráfica de la aceleración de la partícula?
¿En qué intervalos, en s, la partícula está frenando?
¿Cuánto vale, aproximadamente, la rapidez media en el intervalo [0s, 10s]?

2 Desplazamiento neto

Hallamos primero la ecuación de la velocidad como función del tiempo. Por ser una parábola es de la forma

$v = At^2 + B t + C\,$

Como se anula en $t = 2$ y $t = 8$ (segundos, usamos unidades fundamentales del SI) y en $t = 0$ vale -16, queda

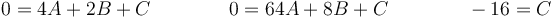
$0 = 4A +2B + C \qquad\qquad 0 = 64A+8B + C\qquad\qquad -16 = C$

Restando

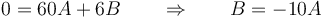
$0 = 60A + 6B\qquad\Rightarrow\qquad B = -10A$

Sustituimos

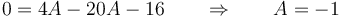
$0 = 4A-20A-16\qquad\Rightarrow\qquad A= -1$

Por tanto la parábola es de la forma

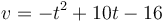
$v = -t^2+10t-16\,$

Integramos respecto al tiempo para hallar el desplazamiento

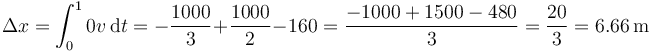
$\Delta x = \int_0^10 v\,\mathrm{d}t = -\frac{1000}{3}+\frac{1000}{2}-160 = \frac{-1000+1500-480}{3}=\frac{20}{3}=6.66\,\mathrm{m}$

3 Gráfica de la aceleración

La velocidad es una función cuadrática, por lo que la aceleración, su derivada, debe ser una recta. Además, la velocidad es creciente en la primera mitad del intervalo y decreciente en la segunda, por lo que la aceleración debe ser poitiva en la primera mitad y negativa en la segunda. Por ello, su gráfica es la B.

Evidentemente, también puede demostrarse derivando respecto al tiempo la expresión de la velocidad.