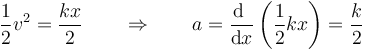Velocidad función de la posición

De Laplace

Revisión a fecha de 08:47 25 sep 2019; Antonio (Discusión | contribuciones)

(dif) ← Revisión anterior | Revisión actual (dif) | Revisión siguiente → (dif)

1 Enunciado

La velocidad de una partícula sigue la ley

$v = \sqrt{Ax}$

siendo $x$ la distancia recorrida desde el instante inicial.

Calcule la aceleración de la partícula. ¿Qué tipo de movimiento describe?

2 Solución

La aceleración la obtenemos derivando la velocidad respecto al tiempo, lo cual se consigue aplicando la regla de la cadena,

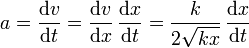
$a = \frac{\mathrm{d}v}{\mathrm{d}t}=\frac{\mathrm{d}v}{\mathrm{d}x}\,\frac{\mathrm{d}x}{\mathrm{d}t}=\frac{k}{2\sqrt{kx}}\,\frac{\mathrm{d}x}{\mathrm{d}t}$

pero la derivada de la posición respecto al tiempo es la propia velocidad, por lo que

$a = \frac{k}{2\sqrt{kx}}\,v = \frac{k}{2\sqrt{kx}}\sqrt{kx} = \frac{k}{2}$

La aceleración es por tanto constante y el movimiento es uniformemente acelerado.

También puede calcularse directamente a partir de la relación

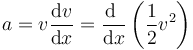
$a = v\frac{\mathrm{d}v}{\mathrm{d}x}=\frac{\mathrm{d}\ }{\mathrm{d}x}\left(\frac{1}{2}v^2\right)$

que en este caso da

$\frac{1}{2}v^2= \frac{kx}{2} \qquad\Rightarrow\qquad a = \frac{\mathrm{d}\ }{\mathrm{d}x}\left(\frac{1}{2}kx\right)=\frac{k}{2}$

Velocidad función de la posición

De Laplace

1 Enunciado

2 Solución

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES