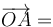1 Enunciado

Se tiene el plano inclinado de la figura que forma un ángulo $θ$ con la horizontal. Se dispara una partícula desde el punto más bajo, con una velocidad inicial $\vec{v}_0$ , de módulo $10 v p$ y con un ángulo $α$ con la horizontal. Los ángulos son tales que

$\mathrm{sen}\,\theta = \dfrac{3}{5}\qquad \cos\theta=\dfrac{4}{5} \qquad\qquad\qquad \mathrm{sen}\,\alpha= \dfrac{4}{5}\qquad \cos\alpha=\dfrac{3}{5}.$

Calcula la distancia $l$ entre el punto de partida y el de impacto sobre el plano inclinado, así como la velocidad (vector) con la que impacta.
Calcula el trabajo realizado por la fuerza gravitatoria sobre la partícula entre los puntos $O$ y $A$ .
Calcula la potencia que la gravedad transmite a la partícula en cada Discute el significado físico del signo de esta potencia.
Calcula las componentes intrínsecas de la aceleración en el punto de impacto.

2 Solución

2.1 Impacto con el plano

La partícula se mueve únicamente bajo la acción de la graveda. Por tanto, su movimiento es un tiro parabólico. La posición y velocidad iniciales son

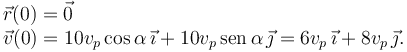
$\begin{array}{l} \vec{r}(0) = \vec{0}\\ \vec{v}(0) = 10v_p\cos\alpha\,\vec{\imath} + 10v_p\,\mathrm{sen}\,\alpha\,\vec{\jmath} = 6v_p\,\vec{\imath} + 8v_p\,\vec{\jmath}. \end{array}$

En el tiro oblicuo, el movimiento horizontal de la partícula es rectilíneo uniforme mientras que el vertical es uniformemente acelerado con aceleración $- g$ . Los vectores aceleración, velocidad y posición de la partícula son

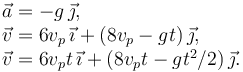
$\begin{array}{l} \vec{a} = -g\,\vec{\jmath},\\ \vec{v} = 6v_p\,\vec{\imath} + (8v_p-gt)\,\vec{\jmath},\\ \vec{v} = 6v_pt\,\vec{\imath} + (8v_pt-gt^2/2)\,\vec{\jmath}.\\ \end{array}$