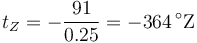Preguntas de test de introducción a la termodinámica (GIE)

De Laplace

Revisión a fecha de 12:44 23 jul 2019; Anamaram (Discusión | contribuciones)

(dif) ← Revisión anterior | Revisión actual (dif) | Revisión siguiente → (dif)

Contenido

1 Temperatura de un gas
2 Temperatura en un proceso
3 Número de psi en una atmósfera
4 Título de una novela en Celsius
5 Densidad del aire húmedo
6 Propiedad termométrica
7 Dilatación de un paralelepípedo
8 Volumen de gasolina
9 Proceso en un gas
10 Dilatación de raíles
11 Dilatación de tapa
12 Escala de temperaturas basada en el metano

1 Temperatura de un gas

Un gas ideal diatómico contenido en un recipiente ocupa un volumen de 500 cm³ a una presión de 4.0 bares y 300 K de temperatura. Experimenta una expansión hasta un estado final en el que ocupa un volumen de 1000 cm³ a una presión de 1.0 bares.

¿Cuál es la temperatura final del gas?

A 150 K
B Depende de si las paredes son adiabáticas o diatermas.
C 75 K
D 600 K

Solución

La respuesta correcta es la A.

La ley de los gases ideales da

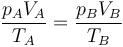
$\frac{p_AV_A}{T_A}=\frac{p_BV_B}{T_B}$

de donde la temperatura final es

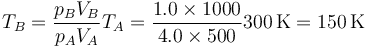
$T_B = \frac{p_BV_B}{p_AV_A}T_A = \frac{1.0\times 1000}{4.0\times 500}300\,\mathrm{K}=150\,\mathrm{K}$

2 Temperatura en un proceso

Se tiene una cantidad fija de un gas ideal diatómico situada a una presión $p 0$ , volumen $V 0$ y temperatura $T 0$ . Experimenta un proceso tal que la presión final es $2 p 0$ y el volumen $2 V 0$ .

En este proceso, la temperatura…

A permanece constante.
B se reduce a la mitad.
C aumenta al doble.
D se multiplica por 4.

Solución

La respuesta correcta es la D.

Como en la pregunta anterior, aplicamos la ley de los gases ideales

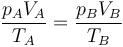
$\frac{p_AV_A}{T_A}=\frac{p_BV_B}{T_B}$

que en este caso da

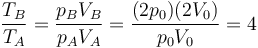
$\frac{T_B}{T_A} = \frac{p_BV_B}{p_AV_A} = \frac{(2p_0)(2V_0)}{p_0V_0}=4$

3 Número de psi en una atmósfera

Una atmósfera equivale a 101325 Pa. Un psi es la presión ejercida por una libra (4.448 N) sobre un cuadrado de lado 1 pulgada (2.54 cm). ¿A cuantos psi equivale una atmósfera?

A 1 atm = 579 psi
B 1 atm = 1.50 psi
C 1 atm = 6894 psi
D 1 atm = 14.7 psi

Solución

La respuesta correcta es la D.

La equivalencia de psi en pascales la obtenemos mediante factores de conversión

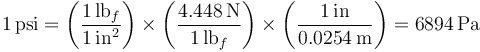
$1\,\mathrm{psi}=\left(\frac{1\,\mathrm{lb}_f}{1\,\mathrm{in}^2}\right)\times\left(\frac{4.448\,\mathrm{N}}{1\,\mathrm{lb}_f}\right)\times\left(\frac{1\,\mathrm{in}}{0.0254\,\mathrm{m}}\right)=6894\,\mathrm{Pa}$

Puesto que una atmósfera son 101325 pascales queda

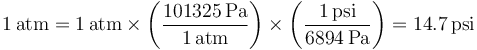
$1\,\mathrm{atm}=1\,\mathrm{atm}\times\left(\frac{101325\,\mathrm{Pa}}{1\,\mathrm{atm}}\right)\times\left(\frac{1\,\mathrm{psi}}{6894\,\mathrm{Pa}}\right)=14.7\,\mathrm{psi}$

4 Título de una novela en Celsius

En el paso de grados Celsius a Fahrenheit se cumple 0°C = 32°F y 100°C = 212 °F. El título de la novela Fahrenheit 451 se refiere a la temperatura a la que arde el papel. ¿Cómo quedaría este título en la escala Celsius?

A Celsius 844
B Celsius 213
C Celsius 251
D Celsius 233

Solución

La respuesta correcta es la D.

La relación entre la temperatura en grados Celsius y en grados Fahrenheit es lineal

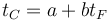
$t_C = a + b t_F\,$

donde los coeficientes los sacamos de que conocemos dos puntos fijos

$0 =a + 32b\qquad\qquad 100 = a + 212b$

de donde

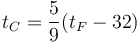
$t_C = \frac{5}{9}(t_F-32)$

Sustituyendo aquí el valor de la temperatura de combustión del papel

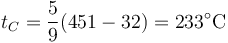
$t_C = \frac{5}{9}(451-32)=233^\circ\mathrm{C}$

5 Densidad del aire húmedo

El aire seco (sin vapor de agua) equivale a un gas ideal de peso molecular 29 g/mol. El agua tiene peso molecular de 18 g/mol. El aire húmedo es el que tiene una cierta cantidad de vapor de agua. A 1 atm y 300 K, ¿qué aire es más denso, el seco o el húmedo?

A Los dos tienen la misma densidad.
B El seco.
C Depende de la humedad del aire.
D El húmedo.

Solución

La respuesta correcta es la B.

Para una presión y temperatura dadas, el número de moles por unidad de volumen esta fijado (según la ley de los gases ideales u otra más complicada en el caso no ideal). Esto quiere decir que el número de moléculas está fijado.

Entonces, cuando entra humedad en el aire seco, las moléculas de agua entran “en lugar de”, no “además de”, es decir, que para mantener constante la presión, por cada molécula de agua que entra, se desaloja una de oxígeno o una de nitrógeno.

Ahora bien, el peso molecular del oxígeno es 32 g/mol y el del nitrógeno 28 g/mol, siendo el del agua solo 18 g/mol. Por tanto, estamos sustituyendo algunas moléculas por otras más ligeras. Consecuentemente, la masa por unidad de volumen, es decir, la densidad, disminuye.

El aire húmedo es entonces más ligero que el aire seco a la misma presión y temperatura.

6 Propiedad termométrica

Se tiene un sistema cerrado que contiene un gas ideal cuya temperatura puede cambiar. ¿Cuál de las siguientes propiedades no nos sirve para construir una escala para un termómetro?

A El número de moles.
B La energía interna.
C La presión.
D El volumen.

Solución

La respuesta correcta es la A.

Según la ley de los gases ideales, cuando se cambia la temperatura, cambia la presión o el volumen. También cambia la energía interna, que depende solo de la temperatura.

Lo único que no cambia con la temperatura es el número de moles, que simplemente nos indica cuantas moléculas hay en el gas. Por ello, el número de moles no se puede usar como propiedad termométrica (que debe ser una función de T).

7 Dilatación de un paralelepípedo

El coeficiente de dilatación lineal del oro a 20 °C es 14×10⁻⁶°C⁻¹. Si se tiene un paralelepípedo de oro que a 20 °C ocupa 500 cm³, ¿cuánto aumenta el volumen cuando se calienta hasta 30 °C?

A 210 mm³
B 140 mm³
C 70 mm³
D 7 mm³

Solución

La respuesta correcta es la A.

La variación lineal de un sólido la da la ley de dilatación

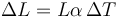
$\Delta L = L\alpha\,\Delta T$

y la volumétrica es

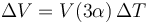
$\Delta V = V(3\alpha)\,\Delta T$

que en este caso vale

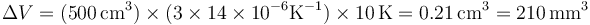
$\Delta V = (500\,\mathrm{cm}^3)\times(3\times 14\times 10^{-6}\mathrm{K}^{-1})\times 10\,\mathrm{K}=0.21\,\mathrm{cm}^3=210\,\mathrm{mm}^3$

8 Volumen de gasolina

Una cierta cantidad de gasolina ocupa 1000 cm³ a 20 °C y 1019 cm³ a 40 °C. ¿Qué volumen ocupa a 80 °C?

A 1095 cm³
B 1057 cm³
C 1038 cm³
D 1076 cm³

Solución

La respuesta correcta es la .

La dilatación de un solido o un líquido es aproximadamente lineal con la temperatura

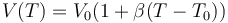
$V(T) = V_0(1+\beta(T-T_0))\,$

lo que nos permite calcular el coeficiente de dilatación $β$

$1019 = 1000(1+\beta(40-20))\qquad\Rightarrow\qquad \beta =9.5\times 10^{-4}\mathrm{K}^{-1}$

y aplicándolo ahora a la temperatura solicitada

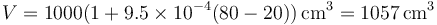
$V = 1000(1+9.5\times 10^{-4}(80-20))\,\mathrm{cm}^3 = 1057\,\mathrm{cm}^3$

De forma más simple, el cálculo es que si subiendo 20 grados aumenta en 19cm³, subiendo 60°C aumenta el triple.

9 Proceso en un gas

Un gas ideal diatómico ocupa un cierto volumen $V 0$ a una presión $p 0$ y una temperatura $T 0$ . Primero, manteniendo constante su volumen, se reduce lentamente su presión a $p 0 / 2$ . Luego, manteniendo constante su nueva presión, se pone gradualmente en contacto con un foco a temperatura $T 0$ . ¿Como se relacionan el volumen inicial, $V 0$ , y final $V f$ , del gas?

A $V f = V 0$
B $V f = V 0 / 2$
C $V f = 2 V 0$
D $V f = 4 V 0$

Solución

La respuesta correcta es la C.

Es simple aplicación de la ley de los gases ideales

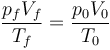
$\frac{p_fV_f}{T_f}=\frac{p_0V_0}{T_0}$

que nos da

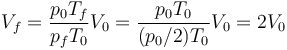
$V_f = \frac{p_0T_f}{p_f T_0}V_0=\frac{p_0T_0}{(p_0/2)T_0}V_0=2V_0$

Nótese que el estado final es independiente del proceso.

10 Dilatación de raíles

Los raíles ferroviarios son de acero y tienen 18 m de longitud a 20°C. Si deben operar entre -10°C y 60°, ¿qué espacio debe dejarse como mínimo entre un tramo y el siguiente si se tienden a una temperatura de 20°?

A 1 cm
B 2 cm
C 2 mm
D 5 mm

Dato: Coeficiente de dilatación lineal del acero: 13×10⁻⁶K⁻⁶

Solución

La respuesta correcta es la A.

Aplicando la ley de la dilatación lineal

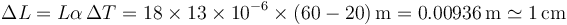
$\Delta L = L\alpha\,\Delta T = 18\times 13\times 10^{-6}\times(60-20)\,\mathrm{m}=0.00936\,\mathrm{m}\simeq 1\,\mathrm{cm}$

Nótese que hay que considerar toda la dilatación lineal de los 18m, y no la mitad (considerando que el raíl se expande en los dos sentidos) ni el doble (considerando que hay dos raíles, uno a continuación del otro). Los dos factores se cancelan. Cada raíl se dilatará 5mm a cada lado, pero al ser dos raíles sucesivos, el espaciado debe ser 5mm + 5mm = 1cm.

11 Dilatación de tapa

Una forma de abrir un bote de vidrio cuya tapa metálica está demasiado apretada consiste en sumergirlo en un baño de agua caliente. Si sumergimos en agua a 60 °C un bote de 4.0 cm de radio con tapa de estaño que a 20 °C encaja perfectamente y el coeficiente de dilatación lineal del vidrio es 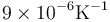$9\times 10^{-6}\mathrm{K}^{-1}$ y el del estaño es 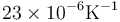$23\times 10^{-6}\mathrm{K}^{-1}$ , ¿cuánta holgura queda al calentarlo?

A 22 μm
B 560 μm
C 37 μm
D 920 μm

Solución

La respuesta correcta es la A.

Aplicamos la ley de dilatación a los radios

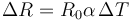
$\Delta R = R_0\alpha\,\Delta T$

puesto que inicialmente los dos tienen el mismo radio y el incremento de temperatura es el mismo para vidrio y tapa, podemos hallar la diferencia entre los diámetros como

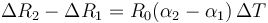
$\Delta R_2-\Delta R_1 = R_0(\alpha_2-\alpha_1)\,\Delta T$

Sustituimos los valores numéricos

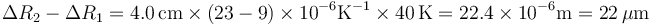
$\Delta R_2-\Delta R_1 = 4.0\,\mathrm{cm}\times(23-9)\times 10^{-6}\mathrm{K}^{-1}\times 40\,\mathrm{K} = 22.4\times 10^{-6}\mathrm{m}=22\,\mu\mathrm{m}$

12 Escala de temperaturas basada en el metano

Zorg, un habitante de Titán, construye una escala de temperaturas basada en el metano tal que a la fusión (91 K) le corresponden 0 °Z y a la ebullición (116 K) 100 °Z. ¿Cuál es la temperatura del cero absoluto en esta escala?

A −187 °Z
B −364 °Z
C −91 °Z
D −25 °Z

Solución

La respuesta correcta es la B.

La relación entre las dos escalas de temperatura es lineal

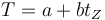
$T = a + b t_Z\,$

Hallamos a y b de los dos puntos conocidos

$91 = a + b\cdot 0\qquad \qquad 116 = a + 100b$

de donde

$a = 91\qquad \qquad b = 0.25$

por lo que la relación es

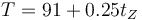
$T = 91 + 0.25t_Z\,$

Para T = 0 queda

$t_Z = -\frac{91}{0.25}= -364\,^\circ\mathrm{Z}$

Preguntas de test de introducción a la termodinámica (GIE)

De Laplace

Contenido

1 Temperatura de un gas

2 Temperatura en un proceso

3 Número de psi en una atmósfera

4 Título de una novela en Celsius

5 Densidad del aire húmedo

6 Propiedad termométrica

7 Dilatación de un paralelepípedo

8 Volumen de gasolina

9 Proceso en un gas

10 Dilatación de raíles

11 Dilatación de tapa

12 Escala de temperaturas basada en el metano

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES