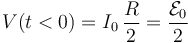Inducción en espira rectangular móvil con voltímetro (F2GIA)

De Laplace

Revisión a fecha de 11:23 5 jul 2019; Gabriel (Discusión | contribuciones)

(dif) ← Revisión anterior | Revisión actual (dif) | Revisión siguiente → (dif)

Contenido

1 Enunciado
2 Solución
- 2.1 (a) Señales eléctricas en la espira antes de entrar en la región magnetizada
  - 2.1.1 Intensidad de la corriente eléctrica en la espira
  - 2.1.2 Voltaje en el centro de la espira

1 Enunciado

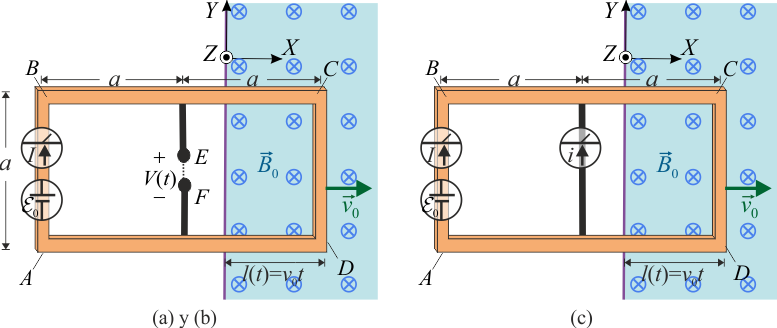
Una espira rectangular $A B C D$ está formada por cuatro conductores filiformes de igual resistividad y sección, y de longitudes $a$ y $2 a$ , siendo $R$ su resistencia eléctrica total. En el lado corto $A B$ tiene incrustado un generador eléctrico ideal con una f.e.m. constante 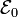$\mathcal{E}_0$ , y con sus electrodos conectados de manera que, por sí sola, generaría una corriente eléctrica que recorrería la espira en sentido horario. Además, en los puntos medios de los lados largos, $B C$ y $D A$ , se conectan sendos conductores filiformes rectilíneos de resistencia nula, paralelos a los lados cortos y que terminan en los extremos $E$ y $F$ , muy próximos pero con una pequeña separación entre ellos, que hace que está rama del circuito esté abierta.

La espira se encuentra siempre contenida en el plano $O X Y$ , con sus lados cortos $A B$ y $C D$ paralelos al eje $O Y$ , y se desplaza con velocidad constante 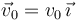$\vec{v}_0=v_0\!\ \vec{\imath}$ , con $v 0 = a / T$ . 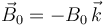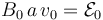Inicialmente, la espira se encuentra en una región donde no existe campo magnético, pero a partir del instante que consideramos $t = 0$ , la espira penetra por su lado corto $C D$ en una región donde existe un campo magnético uniforme $\vec{B}_0=-B_0\!\ \vec{k}$ , cuya intensidad se ajusta de manera que se cumpla $B_0\!\ a\!\ v_0=\mathcal{E}_0$ .

: (a) Para los instantes anteriores a que la espira entre en la región de campo magnético ( $t < 0$ ), determine el valor de la intensidad $I$ (medida en sentido horario) de la corriente eléctrica que recorre la espira. Calcule también el valor del voltaje $V$ entre los extremos $E$ y $F$ .; (b) En los instantes de tiempo $t > 0$ , ¿cómo es la señal de intensidad $I (t)$ de la corriente eléctrica que recorre la espira? ¿Y la señal de voltaje $V (t)$ entre los extremos abiertos $E$ y $F$ ?; (c) Si se repite el experimento pero conectando los extremos $E$ y $F$ mediante un amperímetro de resistencia nula, ¿cómo sería la señal de intensidad de corriente $i (t)$ que registraría dicho amperímetro en los intervalos de tiempo $t < 0$ y $t > 0$ ?

2 Solución

2.1 (a) Señales eléctricas en la espira antes de entrar en la región magnetizada

2.1.1 Intensidad de la corriente eléctrica en la espira

Como primer paso, modelaremos el circuito eléctrico del sistema descrito para instantes de tiempo $t < 0$ ; es decir, antes de que la espira móvil $A B C D$ entre en la región uniformemente magnetizada, que se corresponde con el semiespacio formado por los puntos $P (x, y, z)$ tales que $x < 0$ . En dicha región, es nulo el flujo magnético a través de cualquier superficie $Σ$ que tuviese como contorno a la espira rectangular. 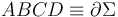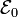Por tanto, la única fuerza electromotriz existente en la espira $ABCD\equiv\partial\Sigma$ es la $\mathcal{E}_0$ del generador eléctrico ideal incrustado en el lado $A B$ .

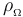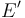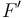Por otra parte, la espira está formada por cuatro barras rectilíneas y filiformes del mismo material óhmico (cuya resistividad tendrá un valor $\rho_{{}_\Omega}$ ), de idéntica sección $S$ y lados iguales dos a dos. Y teniendo en cuenta que los conductores utilizados para medir el voltaje $V (t)$ están conectados a los respectivos centros $E^\prime$ y $F^\prime$ de los lados largos $B C$ y $D A$ , podemos descomponer la espira completa en seis tramos idénticos, filiformes y rectilíneos, también de igual longitud $a$ . En consecuencia, el modelo eléctrico de la espira consistirá en la f.e.m. del generador ideal, conectada a la asociación en serie de seis resistencias eléctricas idénticas 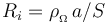$R_i=\rho_{{}_\Omega}\!\ a/S$ , . Y si la resistencia total de la espira es el valor conocido $R$ , se tendrá...

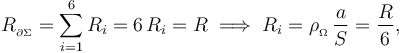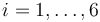
$\displaystyle R_{{}_{\partial\Sigma}}=\sum_{i=1}^6 R_i=6\!\ R_i=R \;\Longrightarrow\; R_i=\rho_{{}_\Omega}\!\ \frac{a}{S}=\frac{R}{6},\;\;\;\;$ para $i=1,\ldots , 6$

De la aplicación de la primera ley de Kirchoff en cada uno de los nodos correspondientes a las conexiones en serie de estas resistencias se obtiene que todas ellas son recorridas por la misma intensidad de corriente eléctrica, que será también la misma que recorre el generador, saliendo por el electrodo positivo de éste y recorriendo el circuito--espira en sentido horario, para el cuál asumiremos que $I (t) > 0$ . La aplicación de la segunda ley de Kirchoff en la malla que se corresponde con la espira permite establecer la ecuación del circuito en $\partial\Sigma$ . Como se trata de un circuito cerrado...

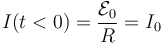
$\left[\sum_j \mathcal{E}_j\right]_{\partial\Sigma}= \sum_{i=1}^6 I_i R_i \;\;\;\longrightarrow\;\;\;\mathcal{E}_0= I(t)\sum_{i=1}^6 R_i=R\!\ I(t)\;\Longrightarrow\;$ $I(t<0)=\frac{\mathcal{E}_0}{R}=I_0$

2.1.2 Voltaje en el centro de la espira

Para determinar el voltaje entre los extremos abiertos (y próximos) $E$ y $F$ , hemos de aplicar la segunda ley de Kirchoff en alguna de las dos mallas que incluyen estos puntos; es decir, la 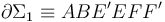$\partial \Sigma_1\equiv ABE^\prime EFF^\prime$ , o bien la 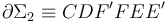$\partial \Sigma_2\equiv CDF^\prime FEE^\prime$ , ambas recorridas en el sentido de intensidad de corriente positiva en la espira conductora. 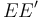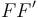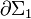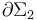Obsérvese que se trata de mallas abiertas: al no existir conexión entre los extremos $E$ y $F$ , no puede haber corriente eléctrica en los cables $EE^\prime$ y $FF^\prime$ ; sin embargo, las mallas $\partial\Sigma_1$ y $\partial\Sigma_2$ están parcialmente recorridas por la corriente eléctrica de intensidad constante $I 0$ en los tramos correspondientes a la espira conductora.

Podemos comprobar que el resultado que se obtiene para la señal de voltaje $V (t) = V E - V F$ es el mismo independientemente de la malla en que se aplique la segunda ley de Kirchoff. Si optamos por la malla 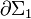$\partial\Sigma_1$ , el modelo de circuito estará constituido por la fuerza electromotriz del generador real (recuérdese que para $t < 0$ no hay f.e.m. 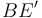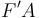inducida en la espira) y las resistencias $R 1$ , $R 2$ y $R 6$ , correspondientes a los tramos de espira $A B$ , $BE^\prime$ y $F^\prime A$ , respectivamente. Por tanto,

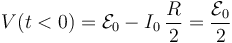
$\left[\sum_j \mathcal{E}_j\right]_{\partial\Sigma_1}= I_0( R_1+R_2+R_6) + V_E-V_F \;\;\;\longrightarrow\;\;\;\mathcal{E}_0= 3\!\ I_0\!\ \frac{R}{6}+V(t)\;\Longrightarrow\;$ $V(t<0)=\mathcal{E}_0-I_0\!\ \frac{R}{2}=\frac{\mathcal{E}_0}{2}$

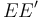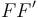Nótese que en los cables $EE^\prime$ y $FF^\prime$ no se produce ninguna caída de tensión o voltaje, ya que por ellos no circula corriente eléctrica al estar en abierto.

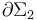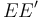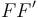Si aplicamos la segunda ley de Kirchoff en la malla abierta $\partial\Sigma_2$ , encontramos que aquí no habría f.e.m. de ningún tipo; sólo los cables $EE^\prime$ y $FF^\prime$ , y las resistencias $R 3$ , $R 4$ y $R 5$ conectadas en serie, que se corresponden con los tramos conductores , 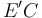$E^\prime C$ , $C D$ y 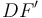$DF^\prime$ . Planteando la ecuación del circuito en esta malla se obtiene...

$\left[\sum_j \mathcal{E}_j\right]_{\partial\Sigma_2}= I_0( R_2+R_4+R_5) + V_F-V_E \;\;\;\longrightarrow\;\;\;0= 3\!\ I_0\!\ \frac{R}{6}-V(t)\;\Longrightarrow\;$ $V(t<0)=I_0\!\ \frac{R}{2}=\frac{\mathcal{E}_0}{2}$

Inducción en espira rectangular móvil con voltímetro (F2GIA)

De Laplace

Contenido

1 Enunciado

2 Solución

2.1 (a) Señales eléctricas en la espira antes de entrar en la región magnetizada

2.1.1 Intensidad de la corriente eléctrica en la espira

2.1.2 Voltaje en el centro de la espira

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES