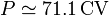Potencia necesaria en un automóvil
De Laplace
1 Enunciado
Calcule la potencia requerida en un automóvil de 1200 kg en las siguientes circunstancias:
- El automóvil sube una pendiente del 6% con rapidez constante de 80 km/h
- El automóvil acelera en un llano de 100 km/h a 120 km/h en 6.0 s.
Suponga que la fuerza de rozamiento promedio es aproximadamente constante e igual a 600 N.
2 Subiendo una pendiente
Para ascender por la pendiente, el coche debe vencer tanto la fuerza de rozamiento como la componente tangencial del peso, la cual apunta hacia abajo de la pendiente. La fuerza que debe ejercer vale entonces
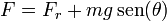
La inclinación de la pendiente es la tangente del ángulo que forma con la horizontal

Vemos que para ángulos tan pequeños, no hay mucha diferencia entre el seno y la tangente (ambos son aproximadamente iguales al ángulo en radianes).
La fuerza que ejerce el coche será
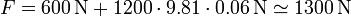
Esta fuerza es ejercida por el coche sobre el suelo y, por la tercera ley de Newton, produce un empuje del suelo sobre el coche capaz de igualar a la fuerza en sentido contrario.
La potencia desarrollada por esta fuerza es igual al producto de la fuerza por la velocidad, que es constante
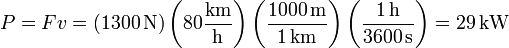
En términos de caballos de potencia, teniendo en cuenta que
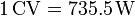
resulta
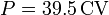
3 Acelerando en recta
En el segundo caso, el coche no debe vencer la acción de la gravedad, pero debe ejercer la fuerza necesaria para acelerar el vehículo, por lo que
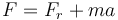
La aceleración media en el tramo es

y la fuerza ejercida vale
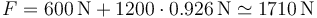
La potencia desarrollada va variando a medida que el coche va aumentando su rapidez. Para hallar su promedio podemos considerar la velocidad media en el tramo

y en caballos de potencia