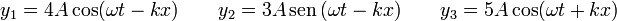Superposición de dos y tres señales

Revisión a fecha de 19:32 10 mar 2009; Antonio (Discusión | contribuciones)

Contenido

Considere los casos de superposición siguientes

$y_1= A \cos(\omega t - kx)\qquad y_2 = A\,\mathrm{sen}\,(\omega t-kx)$
$y_1= A \cos(\omega t - kx)\qquad y_2 = A \,\mathrm{sen}\,(\omega t+kx)$
$y_1= A\cos(\omega t - kx)\qquad y_2 = -2A\,\mathrm{sen}\,(\omega t)\,\mathrm{sen}\,(k x)$
$y_1= 4A\cos(\omega t - kx)\qquad y_2 = 3A\,\mathrm{sen}\,(\omega t-kx)\qquad y_3 = 5A\cos(\omega t + kx )$

Para cada uno de los casos, determine la ecuación de la señal resultante, ¿es una onda viajera o una estacionaria?

$y_1= A \cos(\omega t - kx)\qquad y_2 = A\,\mathrm{sen}\,(\omega t-kx)$

$y_1= A \cos(\omega t - kx)\qquad y_2 = A \,\mathrm{sen}\,(\omega t+kx)$

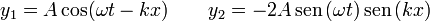
$y_1= A\cos(\omega t - kx)\qquad y_2 = -2A\,\mathrm{sen}\,(\omega t)\,\mathrm{sen}\,(k x)$

$y_1= 4A\cos(\omega t - kx)\qquad y_2 = 3A\,\mathrm{sen}\,(\omega t-kx)\qquad y_3 = 5A\cos(\omega t + kx )$