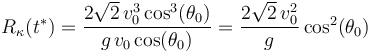No Boletín - Otro tiro parabólico III (Ex.Oct/18)

De Laplace

Revisión a fecha de 00:27 27 mar 2019; Enrique (Discusión | contribuciones)

(dif) ← Revisión anterior | Revisión actual (dif) | Revisión siguiente → (dif)

1 Enunciado

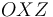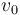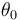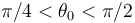Un proyectil se mueve en el plano vertical $OXZ\,$ . Se sabe que tiene una aceleración constante (de módulo $g\,$ ) debida a la gravedad, y que su posición y su velocidad iniciales son las correspondientes a un lanzamiento desde el origen de coordenadas con celeridad inicial $v_{0}\,$ y con un ángulo $\theta_0\,$ sobre el eje horizontal $OX\,$ (siendo $\pi/4<\theta_0<\pi/2\,$ ):

$\vec{a}(t)=-g\vec{k}\,\,\,;\,\,\,\,\,\,\,\,\,\,\,\,\vec{r}(0)=\vec{0}\,\,\,; \,\,\,\,\,\,\,\,\,\,\,\,\vec{v}(0)=v_{0}[\mathrm{cos}(\theta_0)\vec{\imath}+ \mathrm{sen}(\theta_0)\vec{k}\,]$

¿En qué instante 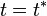$t=t^{*}\,$ tienen valores iguales las aceleraciones tangencial y normal del proyectil $[a_t(t^{*})=a_n(t^{*})]\,$ ?
¿Cuál es el radio de curvatura de la trayectoria del proyectil en el instante definido en la pregunta anterior?

2 Instante en el que tienen valores iguales las aceleraciones tangencial y normal

La definición de aceleración instantánea establece que:

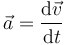
$\vec{a}=\frac{\mathrm{d}\vec{v}}{\mathrm{d}t}$

En el caso que nos ocupa, conocemos el valor inicial de la velocidad 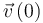$\vec{v}\,(0)\,$ del proyectil, y además conocemos su aceleración en todo instante, la cual tiene valor constante:

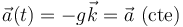
$\vec{a}(t)=-g\vec{k}=\vec{a}\,\,\mathrm{(cte)}$

Determinar la velocidad del proyectil para 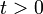$t>0\,$ se reduce a integrar la aceleración entre el instante inicial y un instante genérico:

$\begin{array}{lllll} \mathrm{d}\vec{v}=\vec{a}\,\mathrm{d}t & \,\,\,\,\,\longrightarrow\,\,\,\,\, & \displaystyle\int_{\vec{v}(0)}^{\vec{v}(t)}\!\mathrm{d}\vec{v}=\vec{a}\displaystyle\int_{0}^{\, t}\mathrm{d}t & \,\,\,\,\,\longrightarrow\,\,\,\,\, & \vec{v}(t)=\vec{v}(0)+\vec{a}\,t \end{array}$

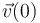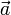Sustituyendo los valores dados de $\vec{v}(0)\,$ y $\vec{a}\,$ , obtenemos:

$\vec{v}(t)=v_0\,\mathrm{cos}(\theta_0)\,\vec{\imath}\,\,+\,\left[v_0\,\mathrm{sen}(\theta_0)-g\;\!t\,\right]\vec{k}$

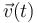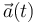Efectuamos el producto escalar y el producto vectorial de $\vec{v}(t)\,$ y $\vec{a}(t)\,$ porque sabemos que dichos productos están presentes en las fórmulas de las componentes intrínsecas de la aceleración:

$\vec{v}(t)\cdot\vec{a}(t)=g\left[g\;\!t-v_0\,\mathrm{sen}(\theta_0)\,\right] \,\,;\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \vec{v}(t)\times\vec{a}(t)=g\;\!v_0\,\mathrm{cos}(\theta_0)\,\vec{\jmath}$

A continuación, igualamos la fórmulas de las aceleraciones tangencial y normal del proyectil para determinar el instante 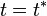$t=t^{*}\,$ en el que ambas componentes intrínsecas tienen valores iguales:

$a_t(t^{*})=a_n(t^{*})\,\,\,\rightarrow\,\,\,\frac{\vec{v}(t^{*})\cdot\vec{a}(t^{*})}{|\vec{v}(t^{*})|}= \frac{|\vec{v}(t^{*})\times\vec{a}(t^{*})|}{|\vec{v}(t^{*})|}\,\,\,\rightarrow\,\,\, g\left[g\;\!t^{*}-v_0\,\mathrm{sen}(\theta_0)\,\right]=g\;\!v_0\,\mathrm{cos}(\theta_0) \,\,\,\rightarrow\,\,\, t^{*}=\displaystyle\frac{v_0}{g}\,[\;\!\mathrm{sen}(\theta_0)\,+\,\mathrm{cos}(\theta_0)\;\!]$

3 Radio de curvatura de la trayectoria en el instante propuesto

Evaluamos la velocidad y la celeridad del proyectil en el instante 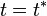$t=t^{*}\,$ :

$\vec{v}(t^{*})=v_0\,\mathrm{cos}(\theta_0)\,\vec{\imath}\,\,+\,\left[v_0\,\mathrm{sen}(\theta_0)-g\;\!t^{*}\,\right]\vec{k}=v_0\,\mathrm{cos}(\theta_0)\,(\vec{\imath}-\vec{k})\,\,\,\,\,\longrightarrow\,\,\,\,\,|\vec{v}(t^{*})|=\sqrt{2}\,v_0\,\mathrm{cos}(\theta_0)$

El radio de curvatura de la trayectoria del proyectil en el instante 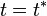$t=t^{*}\,$ puede calcularse a partir de su velocidad y su aceleración en dicho instante mediante la fórmula:

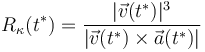
$R_{\kappa}(t^{*})=\frac{|\vec{v}(t^{*})|^3}{|\vec{v}(t^{*})\times\vec{a}(t^{*})|}$

Así que, sustituyendo en dicha fórmula los valores previamente determinados, se obtiene:

$R_{\kappa}(t^{*})=\frac{2\sqrt{2}\,v_0^3\,\mathrm{cos}^3(\theta_0)}{g\;\!v_0\,\mathrm{cos}(\theta_0)}=\frac{2\sqrt{2}\,v_0^2}{g}\,\mathrm{cos}^2(\theta_0)$

No Boletín - Otro tiro parabólico III (Ex.Oct/18)

De Laplace

1 Enunciado

2 Instante en el que tienen valores iguales las aceleraciones tangencial y normal

3 Radio de curvatura de la trayectoria en el instante propuesto

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES