No Boletín - Otro tiro parabólico III (Ex.Oct/18)

De Laplace

Revisión a fecha de 14:18 26 mar 2019; Enrique (Discusión | contribuciones)

(dif) ← Revisión anterior | Revisión actual (dif) | Revisión siguiente → (dif)

1 Enunciado

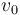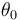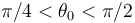Un proyectil se mueve en el plano vertical $OXZ\,$ . Se sabe que tiene una aceleración constante (de módulo $g\,$ ) debida a la gravedad, y que su posición y su velocidad iniciales son las correspondientes a un lanzamiento desde el origen de coordenadas con celeridad inicial $v_{0}\,$ y con un ángulo $\theta_0\,$ sobre el eje horizontal $OX\,$ (siendo $\pi/4<\theta_0<\pi/2\,$ ):

$\vec{a}(t)=-g\vec{k}\,\,\,;\,\,\,\,\,\,\,\,\,\,\,\,\vec{r}(0)=\vec{0}\,\,\,; \,\,\,\,\,\,\,\,\,\,\,\,\vec{v}(0)=v_{0}[\mathrm{cos}(\theta_0)\vec{\imath}+ \mathrm{sen}(\theta_0)\vec{k}]$

¿En qué instante 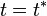$t=t^{*}\,$ tienen valores iguales las aceleraciones tangencial y normal del proyectil $[a_t(t^{*})=a_n(t^{*})]\,$ ?
¿Cuál es el radio de curvatura de la trayectoria del proyectil en el instante definido en la pregunta anterior?

2 Instante en el que tienen valores iguales las aceleraciones tangencial y normal

Las definiciones de velocidad instantánea y aceleración instantánea establecen que:

$\vec{v}=\frac{\mathrm{d}\vec{r}}{\mathrm{d}t}\,\, ;\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \vec{a}=\frac{\mathrm{d}\vec{v}}{\mathrm{d}t}$

En el caso que nos ocupa, conocemos los valores iniciales de la posición 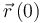$\vec{r}\,(0)\,$ y de la velocidad 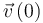$\vec{v}\,(0)\,$ del proyectil, y además conocemos su aceleración en todo instante, la cual tiene valor constante:

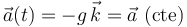
$\vec{a}(t)=-g\,\vec{k}=\vec{a}\,\,\mathrm{(cte)}$

Determinar la velocidad del proyectil para 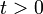$t>0\,$ se reduce a integrar la aceleración entre el instante inicial y un instante genérico:

$\begin{array}{lllll} \mathrm{d}\vec{v}=\vec{a}\,\mathrm{d}t & \,\,\,\,\,\longrightarrow\,\,\,\,\, & \displaystyle\int_{\vec{v}(0)}^{\vec{v}(t)}\!\mathrm{d}\vec{v}=\vec{a}\displaystyle\int_{0}^{\, t}\mathrm{d}t & \,\,\,\,\,\longrightarrow\,\,\,\,\, & \vec{v}(t)=\vec{v}(0)+\vec{a}\,t \end{array}$

Sustituyendo el valor dado de 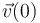$\vec{v}(0)\,$ , obtenemos: