No Boletín - Afirmación falsa II (Ex.Oct/18)

De Laplace

Revisión a fecha de 14:01 23 mar 2019; Enrique (Discusión | contribuciones)

(dif) ← Revisión anterior | Revisión actual (dif) | Revisión siguiente → (dif)

1 Enunciado

Sea la terna de vectores libres:

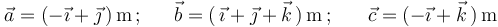
$\vec{a}=(-\vec{\imath}+\vec{\jmath}\,)\,\mbox{m}\,;\,\,\,\,\,\,\,\,\, \vec{b}=(\,\vec{\imath}+\vec{\jmath}+\vec{k}\,)\,\mbox{m}\,;\,\,\,\,\,\,\,\,\, \,\vec{c}=(-\vec{\imath}+\vec{k}\,)\,\mbox{m}$

¿Cuál de las siguientes afirmaciones sobre dicha terna es falsa?

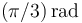(1) Dos de sus vectores forman entre sí un ángulo de $(\pi/3)\,\mathrm{rad}\,$ .

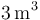(2) Sus tres vectores definen un paralelepípedo de volumen $3\,\mathrm{m}^3\,$ .

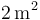(3) Dos de sus vectores definen un paralelogramo de área $2\,\mathrm{m}^2\,$ .

(4) Uno de sus vectores es ortogonal a los otros dos.

2 Solución

Efectuando los productos escalares de las tres parejas posibles de vectores, encontramos que:

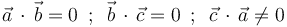
$\vec{a}\,\cdot\,\vec{b}=0\,\,\,;\,\,\,\vec{b}\,\cdot\,\vec{c}=0\,\,\,;\,\,\,\vec{c}\,\cdot\,\vec{a}\neq 0$

Así que el vector 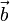$\vec{b}\,$ verifica la condición de ortogonalidad (producto escalar nulo) respecto a los otros dos vectores, y, por tanto, la afirmación (4) es correcta.

A continuación, determinamos el ángulo 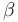$\beta\,$ que forman los dos vectores que no son mutuamente ortogonales ( 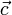$\vec{c}\,$ y $\vec{a}\,$ ):

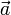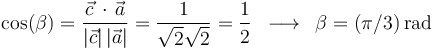
$\mathrm{cos}(\beta)=\displaystyle\frac{\vec{c}\,\cdot\,\vec{a}}{|\vec{c}|\,|\vec{a}|}=\frac{1}{\sqrt{2}\sqrt{2}}=\frac{1}{2}\,\,\,\longrightarrow\,\,\,\beta=(\pi/3)\,\mathrm{rad}$

Por tanto, la afirmación (1) es correcta.

Por otra parte, el volumen del paralelepípedo definido por la terna de vectores libres es igual al valor absoluto de su producto mixto:

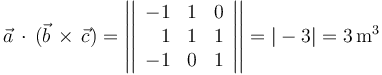
$\vec{a}\,\cdot\,(\vec{b}\,\times\,\vec{c})=\left|\left|\begin{array}{rcc} -1 & 1 & 0 \\ 1 & 1 & 1 \\ -1 & 0 & 1 \end{array}\right|\right|=|-3|=3\,\mathrm{m}^3$

Por tanto, la afirmación (2) es correcta.

Finalmente, determinamos el área del paralelogramo definido por cada pareja posible de vectores calculando el módulo de su producto vectorial:

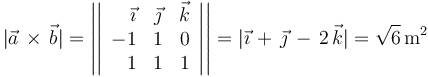
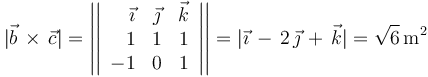
$|\vec{a}\,\times\,\vec{b}|=\left|\left|\begin{array}{rcc} \vec{\imath} & \vec{\jmath} & \vec{k} \\ -1 & 1 & 0 \\ 1 & 1 & 1 \end{array}\right|\right|=|\vec{\imath}\,+\,\vec{\jmath}\,-\,2\,\vec{k}|=\sqrt{6}\,\mathrm{m}^2$ $|\vec{b}\,\times\,\vec{c}|=\left|\left|\begin{array}{rcc} \vec{\imath} & \vec{\jmath} & \vec{k} \\ 1 & 1 & 1 \\ -1 & 0 & 1 \end{array}\right|\right|=|\vec{\imath}\,-\,2\,\vec{\jmath}\,+\,\vec{k}|=\sqrt{6}\,\mathrm{m}^2$ $|\vec{c}\,\times\,\vec{a}|=\left|\left|\begin{array}{rcc} \vec{\imath} & \vec{\jmath} & \vec{k} \\ -1 & 0 & 1 \\ -1 & 1 & 0 \end{array}\right|\right|=|-\,\vec{\imath}\,-\,\vec{\jmath}\,-\,\vec{k}|=\sqrt{3}\,\mathrm{m}^2$

Por tanto, la afirmación (3) es la que es FALSA.

No Boletín - Afirmación falsa II (Ex.Oct/18)

De Laplace

1 Enunciado

2 Solución

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES