No Boletín - Afirmación falsa II (Ex.Oct/18)

De Laplace

Revisión a fecha de 10:45 15 feb 2019; Enrique (Discusión | contribuciones)

(dif) ← Revisión anterior | Revisión actual (dif) | Revisión siguiente → (dif)

1 Enunciado

Sea la terna de vectores libres:

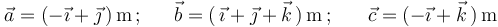
$\vec{a}=(-\vec{\imath}+\vec{\jmath}\,)\,\mbox{m}\,;\,\,\,\,\,\,\,\,\, \vec{b}=(\,\vec{\imath}+\vec{\jmath}+\vec{k}\,)\,\mbox{m}\,;\,\,\,\,\,\,\,\,\, \,\vec{c}=(-\vec{\imath}+\vec{k}\,)\,\mbox{m}$

¿Cuál de las siguientes afirmaciones sobre dicha terna es falsa?

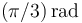(1) Dos de sus vectores forman entre sí un ángulo de $(\pi/3)\,\mathrm{rad}\,$ .

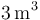(2) Sus tres vectores definen un paralelepípedo de volumen $3\,\mathrm{m}^3\,$ .

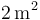(3) Dos de sus vectores definen un paralelogramo de área $2\,\mathrm{m}^2\,$ .

(4) Uno de sus vectores es ortogonal a los otros dos.

2 Solución

No Boletín - Afirmación falsa II (Ex.Oct/18)

De Laplace

1 Enunciado

2 Solución

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES