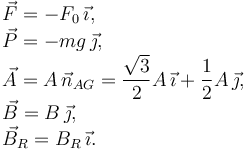De Laplace

1 Enunciado

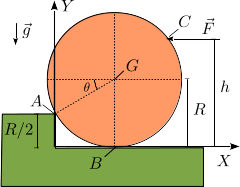
Un disco de radio R y masa m se apoya en un escalón de altura R / 2 como se indica en la figura. El contacto en el punto A es liso mientras que en el punto B es rugoso con coeficiente de rozamiento estático μ. Un fuerza 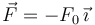, con F₀ > 0, se aplica en el punto C. La gravedad actúa como se indica en la figura.

1. Determina el valor del ángulo θ mostrado en la figura, así como un vector unitario con la dirección y sentido del vector .
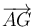2. Dibuja el diagrama de fuerzas que actúan sobre el disco.
3. Encuentra la expresión de las fuerzas que actúan sobre el disco en condición de equilibrio estático. ¿Para que valor de h cambia el sentido de la fuerza de rozamiento?
4. Suponiendo que h = 3R / 2, determina el valor mínimo de F₀ para que el disco suba el escalón.

2 Solución

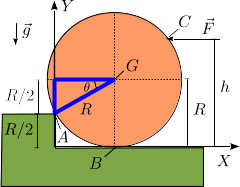
2.1 Ángulo y vector unitario

Observando la figura vemos que, a partir del triángulo resaltado en azul tenemos

El vector 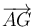es

El módulo de este vector es R, como se observa en la figura. Por tanto, el vector unitario pedido es

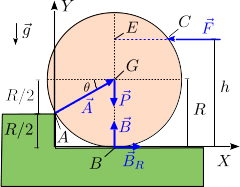
2.2 Diagrama de fuerzas

La figura de la derecha muestra las fuerzas que actúan sobre el sólido. Como fuerzas activas tenemos el peso y . Hay una fuerza vincular en A dirigida hacia el centro del disco, pues en este punto la dirección normal la da la superficie del disco, no la esquina. En el punto B hay una fuerza vincular normal, para que el disco no atraviese el suelo, y una fuerza de rozamiento paralela al suelo. Conocemos a priori el sentido de todas las fuerzas salvo la de rozamiento. Expresamos las fuerzas en el sistema de ejes de la figura