Tren de dos ruedas diferentes (GIE)
De Laplace
Revisión a fecha de 11:32 20 ene 2019; Antonio (Discusión | contribuciones)
Contenido |
1 Enunciado
Un sistema está formado por dos ruedas de masa m y radio R. Una de las ruedas, la trasera es un disco homogéneo, mientras que la delantera es un aro que concentra toda su masa en el borde. Las ruedas están conectadas mediante una varilla de masa despreciable y longitud 4R. Las ruedas están unidas a la varilla mediante rodamientos que permiten el giro sin fricción. Ambas pueden rodar sin deslizar sobre una superficie horizontal en la que el coeficiente de rozamiento estático vale μ. Sea A el centro del disco delantero, B el del trasero, C el de contacto del disco delantero con el suelo y D el del trasero con el suelo.

Se tira del disco delantero mediante una fuerza constante horizontal 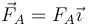 .
.
- Determine la aceleración de los centros de los dos discos cuando se ejerce esta fuerza.
- Halle el valor de las fuerzas sobre los discos en los puntos C y D, de contacto de estos con el suelo, así como la tensión de la varilla.
- Halle el máximo valor que puede tener FA si no se desea que ninguno de los discos deslice. Si se alcanza este valor ¿Cuál es el primer disco que desliza, el delantero, el trasero, o ambos al mismo tiempo?
2 Aceleraciones

3 Fuerzas



4 Deslizamiento inminente
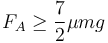
Comienza a deslizar por la rueda delantera.





