De Laplace

Revisión a fecha de 14:10 1 oct 2018; Pedro (Discusión | contribuciones)

(dif) ← Revisión anterior | Revisión actual (dif) | Revisión siguiente → (dif)

1 Enunciado

Dados un vector cualquiera $\vec{A}$ y un vector unitario $\vec{u}$ , expresa el vector $\vec{A}$ como la suma de un vector paralelo a $\vec{u}$ y otro perpendicular a $\vec{u}$ .

2 Solución

Hay que expresar el vector $\vec{A}$ como

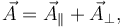
$\vec{A} = \vec{A}_{\parallel} + \vec{A}_{\perp},$

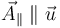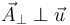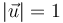donde $\vec{A}_{\parallel}\parallel\vec{u}$ y $\vec{A}_{\perp}\perp\vec{u}$ , siendo $|\vec{u}|=1$ .

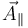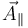Para encontrar $\vec{A}_{\parallel}$ usamos que el producto escalar de $\vec{A}$ por $\vec{u}$ es la proyección de $\vec{A}$ sobre $\vec{u}$ . Para obtener el vector $\vec{A}_{\parallel}$ basta con multiplicar esta proyección por $\vec{u}$

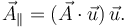
$\vec{A}_{\parallel} = (\vec{A}\cdot\vec{u})\,\vec{u}.$

El módulo de 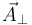$\vec{A}_{\perp}$ se obtiene con el producto vectorial

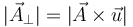
$|\vec{A}_{\perp}| = |\vec{A}\times\vec{u}|$

Debemos hallar un vector unitario 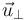$\vec{u}_{\perp}$ que sea perpendicular a $\vec{u}$ y que esté en el plano definido por $\vec{A}$ y $\vec{u}$ . El vector

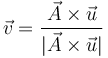
$\vec{v} = \dfrac{\vec{A}\times\vec{u}}{|\vec{A}\times\vec{u}|}$

es unitario y perpendicular al plano definido por $\vec{A}$ y $\vec{u}$ . Entonces

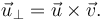
$\vec{u}_{\perp} = \vec{u}\times\vec{v}.$

Entonces

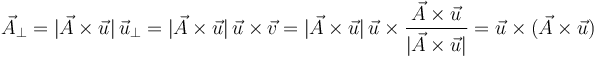
$\vec{A}_{\perp} = |\vec{A}\times\vec{u}|\,\vec{u}_{\perp} = |\vec{A}\times\vec{u}|\,\vec{u}\times\vec{v} = |\vec{A}\times\vec{u}|\,\vec{u}\times\dfrac{\vec{A}\times\vec{u}}{|\vec{A}\times\vec{u}|} = \vec{u}\times(\vec{A}\times\vec{u})$

Es decir

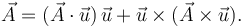
$\vec{A} = (\vec{A}\cdot\vec{u})\,\vec{u} + \vec{u}\times(\vec{A}\times\vec{u}).$

El primer vector es paralelo a $\vec{u}$ y el segundo perpendicular.

Descomposición de un vector (G.I.C.)

De Laplace

1 Enunciado

2 Solución

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES