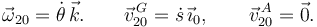Entrar Página Discusión Historial Go to the site toolbox

Sep. 2018 (M.R.) Disco rodando sobre escuadra giratoria

De Laplace

1 Enunciado

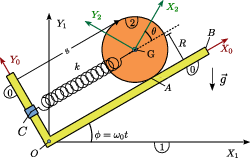
Un disco (sólido "2") de masa M y radio R, rueda sin deslizar sobre una escuadra (sólido "0") de masa despreciable. La escuadra gira en el plano OX1Y1 con velocidad angular constante ω0.

  1. Encuentra reducciones cinemáticas de todos los movimientos del problema en el centro del disco G.
  2. Calcula el momento cinético del disco respecto a G y O, su energía cinética y su energía potencial.
  3. Aplicando los métodos de la Mecánica Vectorial, encuentra las ecuaciones de movimiento del disco. ¿Cuál es la frecuencia propia de oscilación del sistema (también llamada frecuencia natural)?
  4. Encuentra las fuerzas y momentos que actúan sobre la escuadra (sólido "0") para que se mueva de la forma descrita.

2 Solución

2.1 Reducciones cinemáticas

Para el movimiento {01}

\vec{\omega}_{01} = \dot{\phi}\,\vec{k} = \omega_0\,\vec{k}_0, \qquad \vec{v}^{\,O}_{21}=\vec{0}.

El vector geométrico OG es

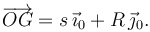
\overrightarrow{OG} = s\,\vec{\imath}_0 + R\,\vec{\jmath}_0.

La velocidad de este movimiento en G es

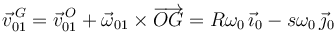
\vec{v}^{\,G}_{01} = \vec{v}^{\,O}_{01} + \vec{\omega}_{01}\times\overrightarrow{OG} = R\omega_0\,\vec{\imath}_0 -s\omega_0\,\vec{\jmath}_0

Para el movimiento {20}

\vec{\omega}_{20} = \dot{\theta}\,\vec{k}. \qquad \vec{v}^{\,G}_{20}=\dot{s}\,\vec{\imath}_0, \qquad \vec{v}^{\,A}_{20}=\vec{0}.

Obtenido de "http://tesla.us.es/wiki/index.php/Sep._2018_(M.R.)_Disco_rodando_sobre_escuadra_giratoria"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Aviso legal - Acerca de Laplace