Test de la 2ª convocatoria CMR 2017-2018
De Laplace
1 Sistema de partículas
En un sistema de partículas sometidas exclusivamente a fuerzas internas newtonianas, ¿cuál de las siguientes cantidades no es una constante de movimiento, en general?
- A La cantidad de movimiento del sistema.
- B El momento cinético respecto al centro de masas del sistema.
- C El momento cinético respecto a un punto fijo O.
- D La energía mecánica del sistema.
- Solución
La respuesta correcta es la D.
Las leyes para un sistema de partículas son
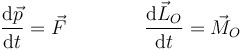
con 
la resultante de las fuerzas externas y 
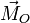el moemnto resultante de las fuerzas externas (O es un punto fijo o el CM). Si no hay fuerzas externas, 
, 
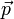y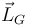 
.
La energía mecánica, en cambio, si puede verse afectada por fuerzas internas. Por ejemplo, el rozamiento entre piezas de un mecanismo frena estos.
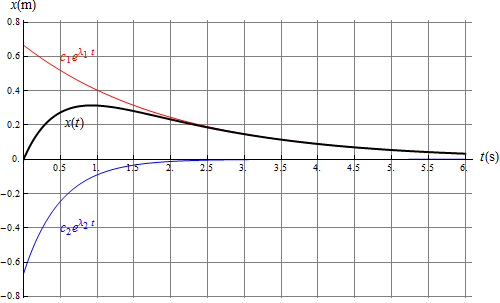
2 Oscilador sobreamortiguado
Un oscilador armónico sobreamortiguado tiene la masa inicialmente en la posición de equilibrio. En ese momento se le comunica una velocidad inicial v_0. ¿Cómo es el movimiento de la masa?
- A Inicialmente se aleja hasta una distancia máxima y luego retorna a la posición inicial de forma más lenta que si el amortiguador fuera crítico.
- B Se va alejando cada vez más lentamente hasta detenerse (tras un tiempo infinito) a una cierta distancia de la posición inicial.
- C Describe un movimiento oscilatorio en el que la amplitud va decayendo exponencialmente con el tiempo.
- D Inicialmente se aleja hasta una distancia máxima y luego retorna a la posición inicial de forma más rápida que si el amortiguador fuera crítico.
- Solución
La respuesta correcta es la A.
Tal como se ve en teoría el comportamiento de un oscilador sobreamortiguado es de la forma
