Proceso cíclico reversible de un gas ideal (F2GIA)
De Laplace
Contenido |
1 Enunciado
Un sistema termodinámico consistente en n moles de un gas ideal monoatómico realiza un proceso cíclico. Inicialmente se encuentra en un estado “A” caracterizado por la terna de valores de presión, volumen y temperatura {P0,V0,T0}. La fase “1” del ciclo consiste en un proceso isócoro (a volumen constante) hasta el estado “B”, en el cuál su temperatura tiene un valor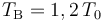 . En la fase “2” se expande isotérmicamente (a temperatura constante), hasta recuperar la presión inicial P0 en el estado “C”. A continuación realiza otro proceso isócoro “3” hasta el estado “D” para, finalmente, realizar un nuevo proceso isotermo “4” que termina en el estado “A”, completando el ciclo. Se asume que todas las fases del ciclo son procesos reversibles.
. En la fase “2” se expande isotérmicamente (a temperatura constante), hasta recuperar la presión inicial P0 en el estado “C”. A continuación realiza otro proceso isócoro “3” hasta el estado “D” para, finalmente, realizar un nuevo proceso isotermo “4” que termina en el estado “A”, completando el ciclo. Se asume que todas las fases del ciclo son procesos reversibles.
- Obtenga los valores de presión, volumen y temperatura en los estados “B”, “C” y “D”, en función de los correspondientes al estado “A”.
- En cada fase del proceso cíclico, calcule las cantidades de energía transferida en forma de calor y de trabajo. Determine también la variación de energía interna en cada fase.
- Calcule el trabajo neto realizado por el sistema en el ciclo (Wout − Win), y las cantidades de calor absorbido (Qin), y cedido (Qout).
- Calcule el rendimiento de esta máquina térmica, definido como el cociente entre el trabajo neto realizado y el calor absorbido en un ciclo. Compárelo con el rendimiento de una máquina térmica de Carnot que trabajase entre los mismos focos térmicos que la analizada.
2 Solución
2.1 Valores de las variables de estado en los estados de equilibrio
Conocidos los valores de presión volumen y temperatura en el estado de equilibrio inicial “A”,
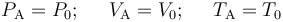
determinamos los valores de estas variables en los otros estados de equilibrio a partir de la descripción del proceso y exigiendo que, en cada uno de esos estados de equilibrio, dichos valores deben verificar la ecuación de estado,
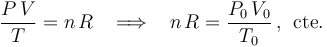
en todos los estados de equilibrio, pues la cantidad de gas (el número 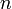 de moles) permanece constante durante todo el proceso, y
de moles) permanece constante durante todo el proceso, y 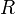 es la constante de los gases ideales, cuyo valor en el Sistema Internacional de unidades es
es la constante de los gases ideales, cuyo valor en el Sistema Internacional de unidades es 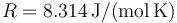 .
.
El proceso que lleva al sistema del estado “A” al “B” se realiza a volumen constante (isócoro), hasta que la temperatura alcanza un determinado valor conocido; por tanto...
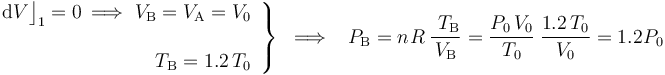
El paso del estado “B” al “C” se realiza manteniéndose constante la temperatura (isotermo), hasta que se recupera la presión del estado inicial “A”:
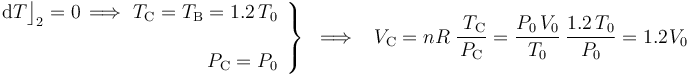
El proceso de “C” a “D” es nuevamente un proceso isócoro en el cuál se mantendrá constante el volumen; es decir, a dichos estados le corresonponde el mismo volumen. Por otra parte, la última fase del proceso cíclico (del estado “D” al “A”) vuelve a ser isoterma; por tanto, ambos estados de equilibrio va a tener igual valor de temperatura. En consecuencia,
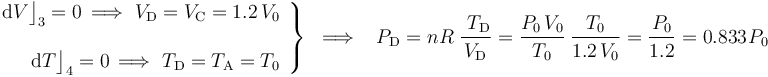
2.2 Energías transferidas a lo largo del proceso
En este apartado se procederá a calcular las cantidades de energía transferida entre el sistema (gas ideal) y el entorno, en forma de calor (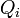 ), y de trabajo (
), y de trabajo (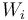 ), en cada una de las cuatro fases (
), en cada una de las cuatro fases (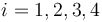 ) del proceso cíclico reversible realizado por el gas.
) del proceso cíclico reversible realizado por el gas.
- Proceso isócoro “1”
Al tratarse de un proceso reversible a volumen constante, la cantidad de energía transferida en forma de trabajo será nula:
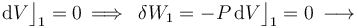
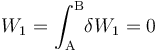
En cuanto al calor transferido, dependerá de la capacidad calorífica a volumen constante 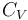 del sistema, consistente en
del sistema, consistente en 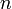 moles de un gas monoátomico:
moles de un gas monoátomico:
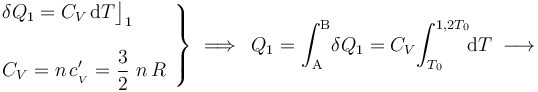
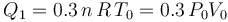
La aplicación del Primer Principio de la Termodinámica determina que la variación de energía interna será igual a la energía transferida en forma de calor:
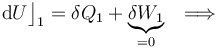
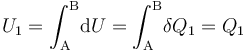
- Proceso isotermo “2”
Como es bien sabido, en un sistema formado por un gas en condiciones de gas ideal, la energía interna del sistema es sólo función de la temperatura. En consecuencia, la variación de aquella magnitud dependerá exclusivamente de la variación que experimente esta variable de estado:
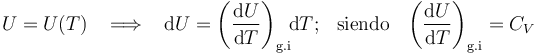
Y como la fase “2” del proceso cíclico bajo estudio se realiza a temperatura constante, la energía interna del sistema también permacenerá invariable. Por tanto, en virtud del Primer Principio de la Termodinámica se tendrá que en este proceso reversible las cantidades de energía transferida en forma de calor y de trabajo serán opuestas:
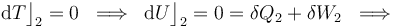
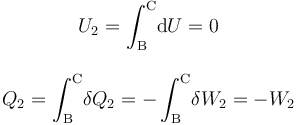
Luego, basta con calcular sólo una de estas cantidades de energía transferida. Como el proceso se realiza a temperatura constante, no es posible determinar el calor transferido a partir de los cambios de esta variable de estado. Sin embargo, al tratarse de un gas ideal que realiza un proceso reversible, consistente en una secuencia de estados de equilibrio en los que se verifica la ecuación de estado, se tendrá:
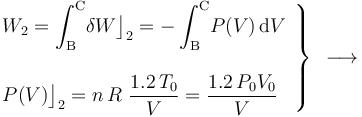
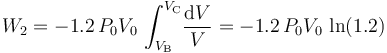
- Proceso isócoro “3”
La fase “3” vuelve a ser un proceso isócoro, en el cual se tendrán resultados anólogos a los obtenidos en “1”, aunque determinados por los valores de las variables de estado en los estados “C” y “D”. Es decir, no habrá energía transferida en forma de trabajo; la transferida en forma de calor está determinada por el cambio de temperatura a volumen constante entre aquellos estados, y coincidirá con la variación de energía interna del sistema:
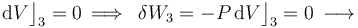
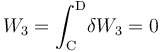
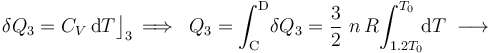
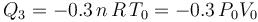
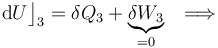
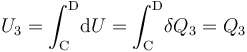
- Proceso isotermo “4”
En el proceso isotermo que cierra el ciclo se obtendrán resultados similares a los de la fase “2”: no hay variación de energía interna, por lo que las cantidades de energía transferidas en forma de calor y de trabajo son opuestas:
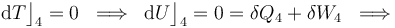
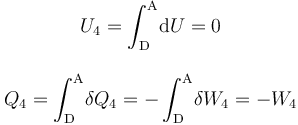
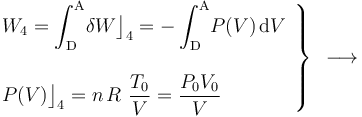
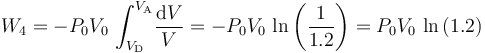
2.3 Trabajo neto por ciclo y calores absorbidos y cedidos por el sistema
El trabajo neto realizado por el sistema sobre entorno en cada ciclo (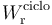 ) es igual a la diferencia entre la cantidad de energía transferida al entorno en forma de trabajo,
) es igual a la diferencia entre la cantidad de energía transferida al entorno en forma de trabajo,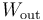 , menos la transferida al sistema en esta misma forma,
, menos la transferida al sistema en esta misma forma, 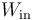 . Atendiendo al criterio de signos empleado a la hora de definir el trabajo en termodinámica, se tendrá que
. Atendiendo al criterio de signos empleado a la hora de definir el trabajo en termodinámica, se tendrá que 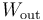 será igual al valor absoluto de la suma de todas las energías en forma de trabajo que tienen signo negativo; es decir, aquéllos que se corresponden con expansiones (aumentos de volumen del sistema). Por el contrario,
será igual al valor absoluto de la suma de todas las energías en forma de trabajo que tienen signo negativo; es decir, aquéllos que se corresponden con expansiones (aumentos de volumen del sistema). Por el contrario, 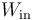 será igual a la suma de todos los trabajos que se corresponden con compresiones del sistema debido a la acción del entorno.
será igual a la suma de todos los trabajos que se corresponden con compresiones del sistema debido a la acción del entorno.
En el sistema bajo estudio, se tiene que el sistema se expande en la fase “2” se comprime en la “4”, mientras que en “1” y “3” no hay transferencia de trabajo. Por tanto,...
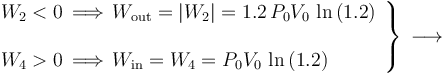
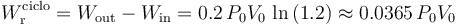
Por su parte, el calor absorbido por el sistema en el ciclo, 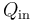 , será igual a la suma de todas las energías transferidas en forma de calor que tengan signo positivo. La suma de los valores absolutos de los calores transferidos con signo negativo será la cantidad de calor cedido por el sistema al entonro
, será igual a la suma de todas las energías transferidas en forma de calor que tengan signo positivo. La suma de los valores absolutos de los calores transferidos con signo negativo será la cantidad de calor cedido por el sistema al entonro 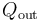 . Por tanto,...
. Por tanto,...
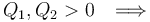
![Q_\mathrm{in}=Q_1+Q_2=[0.3+1.2\!\ \ln\left(1.2\right)]\!\ P_0V_0\approx 0.5188\!\ P_0V_0](/wiki/images/math/5/f/0/5f0d8d3a10b8ce6bd74ecc09c1d7975a.png)
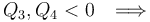
![Q_\mathrm{out}=|Q_3|+|Q_4|=[0.3+\!\ \ln\left(1.2\right)]\!\ P_0V_0\approx 0.4823\!\ P_0V_0](/wiki/images/math/a/d/0/ad0e4272b5868aa698a210bc53dd947b.png)
Como la energía interna es una función de estado, su variación en un proceso cíclico. Y según el Primer Principio de la Termodinámica también deberá ser nula la suma del calor y el trabajo transferidos al sistema desde el entorno menos la suma del calor y el trabajo transferidos al entorno desde el sistema:
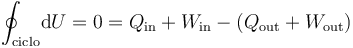
Obsérvese que los resultados obtenidos en este apartado son consistentes con estas consideraciones:
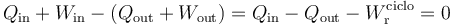
2.4 Rendimiento de la máquina térmica
El sistema descrito de 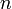 moldes de gas ideal que realiza un proceso cíclico, absorbiendo calor del entorno en una parte del ciclo y cediéndolo al mismo en otra, y realizando un trabajo neto sobre aquél, constituye un máquina térmica. Y puesto que el valor de la temperatura del sistema en todo el ciclo va a estar comprendida en el intervalo
moldes de gas ideal que realiza un proceso cíclico, absorbiendo calor del entorno en una parte del ciclo y cediéndolo al mismo en otra, y realizando un trabajo neto sobre aquél, constituye un máquina térmica. Y puesto que el valor de la temperatura del sistema en todo el ciclo va a estar comprendida en el intervalo
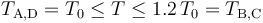
podemos considerar que dichos valores extremos se corresponden con las temperaturas de los focos frío y caliente con los que intercambia calor.
Por definición, el rendimiento de la máquina (real) bajo estudio es:
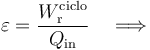
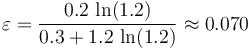
Comparemos este rendimiento con el que tendría una máquina de Carnot que trabajase entre idénticos focos térmicos. Es decir, una máquina que realizase un ciclo formado por los siguientes procesos reversibles: una expansión isoterma del gas a temperatura 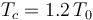 ; una segunda expansión, pero adiabática (sin transferirse calor entre sistema y entorno) hasta enfriarse a la temperatura Tf = T0; una compresión isoterma a esta temperatura y, finalmente, una compresión adiabática por la cual el sistema recupera el estado inicial a temperatura No se pudo entender (Falta el ejecutable de <strong>texvc</strong>. Por favor, lea <em>math/README</em> para configurarlo.): 1.2\!\T_0
. Se puede demostrar que una máquina que realizase este proceso cíclico ideal, tendría un rendimiento tal que
; una segunda expansión, pero adiabática (sin transferirse calor entre sistema y entorno) hasta enfriarse a la temperatura Tf = T0; una compresión isoterma a esta temperatura y, finalmente, una compresión adiabática por la cual el sistema recupera el estado inicial a temperatura No se pudo entender (Falta el ejecutable de <strong>texvc</strong>. Por favor, lea <em>math/README</em> para configurarlo.): 1.2\!\T_0
. Se puede demostrar que una máquina que realizase este proceso cíclico ideal, tendría un rendimiento tal que
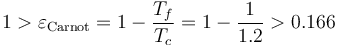
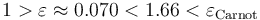
Se cumple entonces que el rendimiento de la máquina (real) bajo estudio tiene un rendimiento menor que la máquina reversible de Carnot que trabaja intercambiando calor con idénticos focos frío y caliente, tal como establece el Segundo principio de la Termodinámica.






