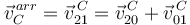De Laplace

Revisión a fecha de 12:13 17 jul 2018; Pedro (Discusión | contribuciones)

(dif) ← Revisión anterior | Revisión actual (dif) | Revisión siguiente → (dif)

Contenido

1 Desplazamientos virtuales

1 Desplazamientos virtuales

El concepto de desplazamiento virtual es fundamental para entender la Mecánica Analítica. Un desplazamiento virtual es un movimiento de cualquier parte de un sistema mecánico que sea compatible con las ligaduras, suponiendo que el tiempo se congela.

1.1 Desplazamientos virtuales para sistemas de partículas

Vamos a empezar con un ejemplo sencillo. Tenemos una partícula engarzada en un aro de radio $R$ centrado en el origen y situado en el plano $O X Y$ . Las ligaduras son esclerónomas:

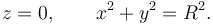
$z=0, \qquad x^2+y^2=R^2.$

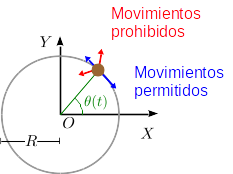
Si se aplica una fuerza sobre partícula (la gravedad u otra) esta realizará un movimiento. Este es el movimiento real de la partícula. Cómo es el movimiento real depende de la fuerza que se ejerza. Pero imaginemos que congelamos el tiempo, como si en una película mostrando el movimiento extraemos uno de los fotogramas y lo mostramos aparte. Mirando el fotograma nos preguntamos: ¿que movimiento podría realizar la partícula en este instante? Tiene que ser un movimiento que respete las ligaduras, en este caso, que esté en el plano $O X Y$ y la distancia al origen sea $R$ . Las flechas azules muestran movimientos posibles, mientras que las rojas muestran movimientos prohibidos. Los movimientos permitidos en esta circunstancia, con el tiempo congelado, son los desplazamientos virtuales. No dependen de las fuerzas activas a las que esté sometida la partícula. En general, hay un número infinito de desplazamientos virtuales. En este caso, el ángulo podría cambiar en 1 grado o en 10, en un sentido o en el otro. Todos esos movimientos respetarían las ligaduras. Fijémonos que el desplazamiento real que realice la partícula bajo la acción de una fuerza dada coincidirá con uno de los posibles desplazamientos virtuales. Esto es cierto si el sistema es esclerónomo.

¿Cómo podemos expresar matemáticamente los desplazamientos virtuales? Nos limitaremos a desplazamientos virtuales infinitesimales, que son los útiles en Mecánica. Ya hemos visto que este sistema tiene un grado de libertad: ${θ}$ . El vector de posición de la partícula puede escribirse como

$\vec{r} = R\cos\theta\,\vec{\imath} + R\,\mathrm{sen}\,\theta\,\vec{\jmath}.$

Un desplazamiento virtual corresponde a una variación infinitesimales del grado de libertad. Si el ángulo cambia en un $δθ$ pequeño el cambio del vector de posición es

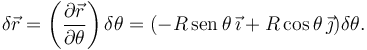
$\delta\vec{r} = \left(\dfrac{\partial\vec{r}}{\partial\theta}\right)\delta\theta = (-R\,\mathrm{sen}\,\theta\,\vec{\imath} + R\cos\theta\,\vec{\jmath})\delta\theta.$

Este es un vector tangente al vínculo (la circunferencia) como los vectores azules de la figura. Para cada valor de $δθ$ (positivo o negativo) tenemos un desplazamiento virtual posible.

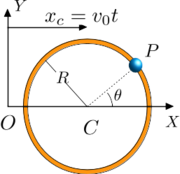
Consideremos ahora un vínculo reónomo, como el de la figura de la derecha. Imaginamos de nuevo que extraemos un fotograma de la película que muestra un movimiento real de la partícula y nos preguntamos cuales son los movimientos posibles en el fotograma, con el tiempo congelado. De nuevo, los movimientos posibles son tangentes a la circunferencia en ese instante. EL vector de posición de la partícula es

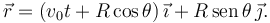
$\vec{r} = (v_0t + R\cos\theta)\,\vec{\imath} + R\,\mathrm{sen}\,\theta\,\vec{\jmath}.$

En el desplazamiento virtual sólo cambia el valor de la coordenada generalizada $θ$ , pero no del tiempo. Para obtener la expresión del desplazamiento virtual tenemos que derivar respecto a $θ$ sin variar $t$

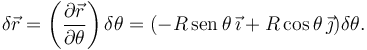
$\delta\vec{r} = \left(\dfrac{\partial\vec{r}}{\partial\theta}\right)\delta\theta = (-R\,\mathrm{sen}\,\theta\,\vec{\imath} + R\cos\theta\,\vec{\jmath})\delta\theta.$

En este caso el movimiento real no puede coincidir con ninguno de los desplazamientos virtuales. El desplazamiento real tiene una componente horizontal que no respeta el vínculo. Esto ocurre en los sistemas reónomos.

Consideremos ahora el péndulo plano con muelle que hemos visto antes. Hay dos grados de libertad: ${r,θ}$ . El vector de posición es

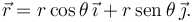
$\vec{r} = r\cos\theta\,\vec{\imath} + r\,\mathrm{sen}\,\theta\,\vec{\jmath}.$

El desplazamiento virtual mas general posible es

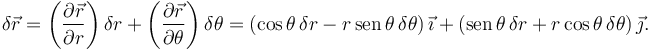
$\delta\vec{r} = \left(\dfrac{\partial\vec{r}}{\partial r}\right)\delta r + \left(\dfrac{\partial\vec{r}}{\partial\theta}\right)\delta\theta = (\cos\theta\,\delta r - r\,\mathrm{sen}\,\theta\,\delta\theta)\,\vec{\imath} + (\mathrm{sen}\,\theta\,\delta r + r\cos\theta\,\delta\theta)\,\vec{\jmath}.$

Cualquier combinación de valores para ${δ r,δθ}$ es un desplazamiento virtual. Por ejemplo

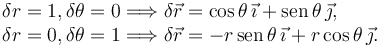
$\begin{array}{l} \delta r=1, \delta\theta = 0 \Longrightarrow \delta\vec{r} = \cos\theta\,\vec{\imath} + \mathrm{sen}\,\theta\,\vec{\jmath}, \\ \delta r=0, \delta\theta = 1 \Longrightarrow \delta\vec{r} = -r\,\mathrm{sen}\,\theta\,\vec{\imath} + r\cos\theta\,\vec{\jmath}. \end{array}$

En el primer caso $θ$ es constante y la partícula se mueve siguiendo la línea radial. En el segundo $r$ es constante y la partícula se mueve tangencialmente a una circunferencia de radio $r$ .

En el caso más general, si tenemos un sistema de $N$ partículas, descrito por un conjunto de $n$ coordenadas generalizadas $\{q_1, \ldots, q_n\}$ con vectores de posición dados por

$\vec{r}_i = \vec{r}_i(q_1, \ldots, q_n, t)\qquad i=1, \ldots, N$

un desplazamiento virtual es un conjunto de variaciones infinitesimales de las coordenadas generalizadas:

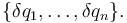
$\{\delta q_1, \ldots, \delta q_n\}.$

Para cada partícula del sistema tenemos

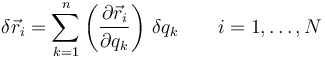
$\delta\vec{r}_i = \sum\limits_{k=1}^{n} \left( \dfrac{\partial\vec{r}_i}{\partial q_k}\right)\,\delta q_k \qquad i=1, \ldots, N$

A partir de ahora, para abreviar denominaremos el conjunto de $n$ coordenadas generalizadas utilizadas para describir un sistema y un desplazamiento virtual genérico respectivamente como

$\{q_k\}\equiv \{q_1,\ldots,q_n\}, \qquad \{\delta q_k\}\equiv\{\delta q_1,\ldots,\delta q_n\}$

1.2 Desplazamientos virtuales con sólidos rígidos

Si tenemos un sistema de sólidos rígidos descrito por un conjunto de coordenadas generalizadas ${q k}$ , un desplazamiento virtual es un conjunto de variaciones infinitesimales de esas coordenadas: ${δ q k}$ . Para cada punto $P$ del sistema, con vector de posición 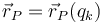$\vec{r}_P= \vec{r}_P(q_k)$ , el desplazamiento virtual se escribe

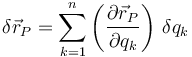
$\delta\vec{r}_P = \sum\limits_{k=1}^{n} \left( \dfrac{\partial\vec{r}_P}{\partial q_k}\right)\,\delta q_k$

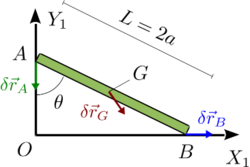
En la figura tenemos una barra que realiza un movimiento plano apoyada en el suelo y una pared. El sólido tiene un grado de libertad

$n=1, \qquad \{q=\theta\}.$

Los vectores de posición de los puntos $A, B, G$ son

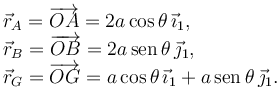
$\begin{array}{l} \vec{r}_A = \overrightarrow{OA} = 2a\cos\theta\,\vec{\imath}_1,\\ \vec{r}_B = \overrightarrow{OB} = 2a\,\mathrm{sen}\,\theta\,\vec{\jmath}_1,\\ \vec{r}_G = \overrightarrow{OG}= a\cos\theta\,\vec{\imath}_1 + a\,\mathrm{sen}\,\theta\,\vec{\jmath}_1. \end{array}$

Para un desplazamiento virtual ${δθ}$ tenemos

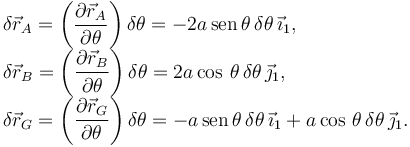
$\begin{array}{l} \delta\vec{r}_A = \left(\dfrac{\partial\vec{r}_A}{\partial\theta}\right)\delta\theta= -2a\,\mathrm{sen}\,\theta\,\delta\theta\,\vec{\imath}_1,\\ \delta\vec{r}_B = \left(\dfrac{\partial\vec{r}_B}{\partial\theta}\right)\delta\theta= 2a\cos\,\theta\,\delta\theta\,\vec{\jmath}_1,\\ \delta\vec{r}_G = \left(\dfrac{\partial\vec{r}_G}{\partial\theta}\right)\delta\theta= -a\,\mathrm{sen}\,\theta\,\delta\theta\,\vec{\imath}_1 + a\cos\,\theta\,\delta\theta\,\vec{\jmath}_1. \end{array}$

Los vectores de la figura corresponden a un desplazamiento virtual con $δθ > 0$ .

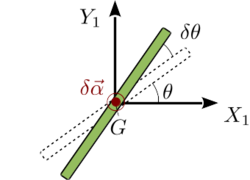
Al trabajar con sólidos rígidos es interesante definir el concepto de rotación virtual: una rotación infinitesimal que sea compatible con las ligaduras con el tiempo congelado. Una rotación virtual se describe matemáticamente con un vector cuya dirección coincida con el eje de rotación, su magnitud con el ángulo rotado y su sentido con el dado por la regla de la mano derecha. La figura de la derecha representa una barra articulada en su centro de modo que sólo puede hacer una rotación respecto al eje $G Z 1$ . El sistema tiene un grado de libertad: ${θ}$ . Una rotación virtual se representa por

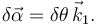
$\delta\vec{\alpha} = \delta\theta\,\vec{k}_1.$

1.3 Velocidades virtuales

Otra forma de abordar los movimientos virtuales de un sistema es utilizando el concepto de velocidades virtuales. La idea es similar a la de los desplazamientos virtuales. Dado un sistema mecánico sometido a ligaduras, examinamos el sistema en un instante dado. Las velocidades virtuales son aquellas compatibles con las ligaduras en ese instante, pero excluyendo el movimiento de arrastre debido a las ligaduras reónomas que haya en el sistema. Es decir, en las velocidades virtuales sólo aparecen las derivadas temporales de las coordenadas generalizadas.

Consideremos de nuevo la partícula engarzada en un aro con movimiento prefijado. El vector de posición de la partícula es

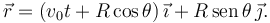
$\vec{r} = (v_0t + R\cos\theta)\,\vec{\imath} + R\,\mathrm{sen}\,\theta\,\vec{\jmath}.$

La velocidad virtual es la que se obtendría de la variación de las coordenadas generalizadas, dejando congelado el tiempo

$\vec{v}^{\,*} = \left(\dfrac{\partial\vec{r}}{\partial\theta}\right)\,\dot{\theta} = \dot{\theta}\,(-R\,\mathrm{sen}\,\theta\,\vec{\imath} + R\cos\theta\,\vec{\jmath})$

La velocidad debida al movimiento del vínculo es la velocidad de arrastre

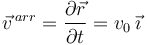
$\vec{v}^{\,arr} = \dfrac{\partial\vec{r}}{\partial t} = v_0\,\vec{\imath}$

En la figura se muestra una posible velocidad virtual en azul y la velocidad de arrastre en verde.

En general, para un sistema con $n$ coordenadas generalizadas ${q k}$ , las velocidades virtual y de arrastre de un punto del sistema con vector de posición $\vec{r}(q_k,t)$ son

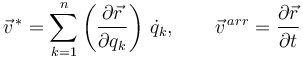
$\vec{v}^{\,*} = \sum\limits_{k=1}^n \left(\dfrac{\partial\vec{r}}{\partial q_k}\right)\,\dot{q}_k, \qquad \vec{v}^{\,arr} = \dfrac{\partial\vec{r}}{\partial t}$

Las velocidades generalizadas son paralelas a los desplazamientos virtuales

$\delta\vec{r} = \vec{v}^{\,*}\delta t.$

Este $δ t$ es una especie de intervalo de tiempo virtual.

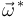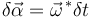Si tratamos con un sólido rígido aparece de manera análoga el concepto de velocidad de rotación virtual $\vec{\omega}^{\,*}$ . Tenemos también $\delta\vec{\alpha} = \vec{\omega}^{\,*}\delta t$ .

En ocasiones es mas sencillo calcular las velocidades virtuales y, a partir de ellas, obtener la expresión de los desplazamientos virtuales multiplicando por ese $δ t$ . Esto es especialmente cierto cuando estudiamos sistemas de sólidos rígidos, pues entonces podemos aplicar las técnicas de movimiento relativo estudiadas en temas anteriores.

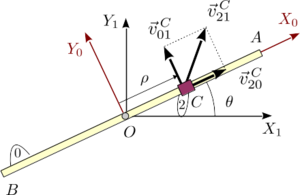
Como ejemplo, tomemos el sistema de la derecha. La barra (sólido "0") puede rotar alrededor de su centro, que es un punto fijo. El deslizador (sólido "2") puede moverse libremente a lo largo de la barra. La configuración del sistema puede describirse con el sistema de coordenadas generalizadas ${ρ,θ}$ . La figura muestra los ejes asociados al sólido "0" y al sólido fijo "1". Consideremos cuatro situaciones posibles

1: ${ρ$ libre, $θ$ libre}: el sistema tiene dos grados de libertad. No hay velocidad de arrastre y la velocidad virtual puede expresarse como

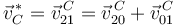
$\vec{v}_C^{\,*} = \vec{v}_{21}^{\,C} = \vec{v}_{20}^{\,C} + \vec{v}_{01}^{\,C}$

2: ${ρ$ libre, $θ = ω 0 t$ }: la coordenada $θ$ no es un grado de libertad, pues su dependencia con el tiempo está prefijada. El sistema tiene un grado de libertad. Las velocidades de arrastre y virtual se expresan como

$\vec{v}^{\,arr}_C = \vec{v}^{\,C}_{01}, \qquad \vec{v}^{\,*}_C = \vec{v}^{\,C}_{20}$

3: ${ρ = v 0 t$ , $θ = ω 0 t$ }: la coordenada $ρ$ no es un grado de libertad, pues su dependencia con el tiempo está prefijada. El sistema tiene un grado de libertad. Las velocidades de arrastre y virtual se expresan como

$\vec{v}^{\,arr}_C = \vec{v}^{\,C}_{20}, \qquad \vec{v}^{\,*}_C = \vec{v}^{\,C}_{01}$

4: ${ρ = v 0 t,θ = ω 0 t$ }: las dos coordenadas tienen su dependencia con el tiempo prefijada. El sistema no tiene grados de libertad. No hay velocidad virtual posible y la velocidad de arrastre es

$\vec{v}^{\,arr}_C = \vec{v}^{\,C}_{21} = \vec{v}^{\,C}_{20} + \vec{v}^{\,C}_{01}$

MR 09 Desplazamientos virtuales

De Laplace

Contenido

1 Desplazamientos virtuales

1.1 Desplazamientos virtuales para sistemas de partículas

1.2 Desplazamientos virtuales con sólidos rígidos

1.3 Velocidades virtuales

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES