Determinación del material de un cable conductor (GIA)
De Laplace
1 Enunciado
Un conductor filiforme, de un material desconocido, tiene una
sección uniforme de área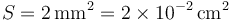 
. Para determinar el tipo de material, se hace
que por el hilo conductor circule una corriente estacionaria de
intensidad 
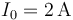y, con la ayuda de un voltímetro,
se determinan dos puntos A y B en el hilo tales que la diferencia
de potencial entre ellos sea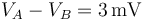 
. Se determina que la longitud del hilo comprendida entre dichos puntos es 
.
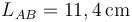- Calcule la esistividad del hilo e indique de qué material está fabricado.
- Haga una estimación de los valores de la intensidad del campo el\'{e}ctrico
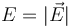), y de la densidad volumétrica (
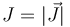), en el interior del cable.
2 Solución
- Planteamiento
Como sabemos, un conductor filiforme (o cable) es un medio óhmico, caracterizado por una conductividad eléctrica No se pudo entender (Falta el ejecutable de <strong>texvc</strong>. Por favor, lea <em>math/README</em> para configurarlo.): \sigma_{{}_\Omega}}
, cuya geometría puede ser identificada con una curva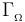 
en el espacio. Para ello, la sección S del cable debe ser suficientemente pequeña frente a otras dimensiones del medio. Asumiendo que éste se encuentra inmerso en una región dieléctrica (vacío, aire,...) se tendrá que, cuando es sometido a un campo eléctrico 
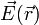(por ejemplo, estableciendo entre sus extremos se establece una diferencia de potencial al conectarlos a sendos electrodos de un generador eléctrico), la densidad volumétrica de corriente 
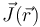que caracteriza el movimiento de cargas eléctricas en el cable es un campo vectorial cuyas líneas de campo están confinadas en la región filiforme 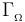; en el límite 
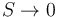, puede considerarse que el medio óhmico filiforme coincide con una línea del campo .
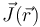Si se consideran dos puntos A y B del conductor filiforme, que prácticamente coincidirán con sendas secciones equipotenciales SA y SB del mismo, el segmento de cable comprendido entre dicho puntos constituye un tubo de corriente. Por definición, la resistencia eléctrica de dicho segmento de conductor es la relación existente entre la diferencia de potencial entre dichos puntos, y la intensidad de la corriente electrica que recorre el conductor:
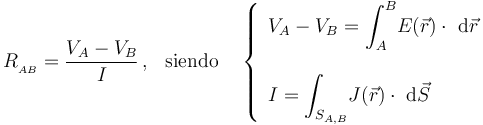
La geometría filiforme del conducor
