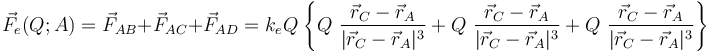Fuerza eléctrica en sistema de cuatro cargas puntuales (GIA)
De Laplace
Contenido |
1 Enunciado
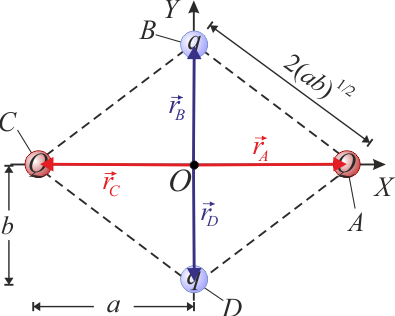
Dos cargas eléctricas puntuales idénticas de valor Q, ocupan sendos puntos A y C que, en un sistema de referencia $OXYZ$, tienen coordenadas cartesianas A(a,0,0) y C( − a,0,0). Otras dos cargas idénticas entre sí y de valor q, ocupan los puntos B y D del eje OY, cuyas coordenadas cartesianas son B(0,b,0) y D(0, − b,0). La geometríadel sistema es tal que la distancia que separa dos carta contiguas es
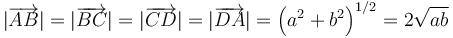
No existen más cargas eléctricas, a parte de las cuatro que constituyen el sistema descrito.
- ¿Qué relación deben verificar la cantidades de Q y q de las respectivas cargas puntuales descritas en el sistema para que la fuerza eléctrica resultante que actúa sobre la carga que ocupa el punto A sea nula,
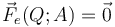 ?
?
- En las condiciones del apartado anterior, ¿cómo es la fuerza eléctrica resultante que actúa sobre cada una de las otras tres cargas?
2 Solución
2.1 Introducción
La ley de Coulomb establece describe cómo es la fuerza de interacción entre dos cargas eléctricas puntales, con valores q1 y q2, situadas en sendos puntos P1y P2 del espacio vacío cuyas posiciones, respecto del origen O de uns sistema de referencia fijo OXYZ, están determinadas por los vectores 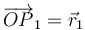 y
y 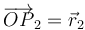 . El módulo, la dirección y el sentido de la fuerza
. El módulo, la dirección y el sentido de la fuerza 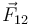 que la carga q2 ejerce sobre q1, responden a la expresión vectorial
que la carga q2 ejerce sobre q1, responden a la expresión vectorial
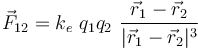
donde ke es el correspondiente factor de escala, denominado constante electrostática y cuyo valor dependerá del sistema de unidades utilizado. Si las magnitudes físicas se expresan en el Sistema Internacional, el valor de esta constante es 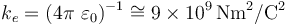 .
.
Las fuerzas de interacción entre cargas eléctricas verifica, el principio de acción y reacción por lo que, simultáneamente se tendrá que la fuerza ejercida por la carga q1 sobre la q2 será opuesta a la anterior; es decir, 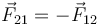 .
.
Por otra parte, la fuerza eléctrica verifica el principio de superposición. por tanto, si se tiene un sistema formado por un conjunto de N cargas puntuales, 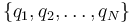 , situadas en los puntos respectivos
, situadas en los puntos respectivos 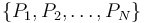 del espacio vacío, la fuerza eléctrica total ejercicida por dicho sistema sobre otra carga puntual q0 situada en un punto P0 del espacio, es igual a la suma vectorial de las fuerzas que cada una de las cargas qi (con
del espacio vacío, la fuerza eléctrica total ejercicida por dicho sistema sobre otra carga puntual q0 situada en un punto P0 del espacio, es igual a la suma vectorial de las fuerzas que cada una de las cargas qi (con 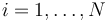 ) ejercerían por sí solas sobre q0:
) ejercerían por sí solas sobre q0:
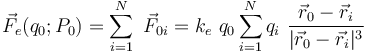
donde 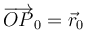 y
y 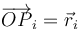 , para
, para 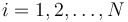 .
.
2.2 Condición para fuerza nula sobre la carga en A
En el ejercicio se propone un sistema formado por cuatro cargas eléctricas, iguales dos a dos,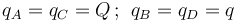
situadas en los vértices A, B, C y D, de dimensiones conocidas y tales que, si se utiliza el sistema de referencia cartesiano indicado en la figura, las posiciones de estos cuatro puntos están dadas por los vectores:
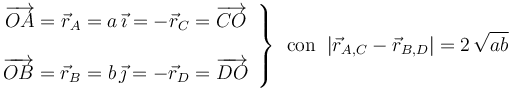
En virtud del principio de superposción y de la ley de Coulomb se tendrá que la fuerza eléctrica resultante que actúa sobre la carga Q situada en el punto A es: