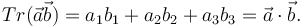Cálculo con diadas
De Laplace
1 Introducción
Una diada es un ente matemático tensorial que se define a partir del producto diádico de dos vectores. Es útil para expresar magnitudes físicas vectoriales, como el Tensor de Inercia, el momento cuadrupolar, el Tensor de Tensiones de Maxwell, etc. Vamos a definir el producto diádico y ver como se aplica en la Mecánica del Sólido Rígido
2 Producto diádico de dos vectores
Consideremos los vectores  y
y  con componentes cartesianas
con componentes cartesianas
![\vec{a} = [a_1, a_2, a_3], \qquad
\vec{b} = [b_1, b_2, b_3]](/wiki/images/math/3/d/3/3d30d4796d9e015c5a8c218916c72e18.png)
Usaremos también el traspuesto de un vector
![\vec{a}^T =
\left[
\begin{array}{c}
a_1 \\ a_2 \\ a_3
\end{array}
\right]
\qquad\qquad
\vec{b}^T =
\left[
\begin{array}{c}
b_1 \\ b_2 \\ b_3
\end{array}
\right]](/wiki/images/math/1/5/d/15dcd613f42a2f4ae0c3193f8e0a69c7.png)
En el espacio  y con coordenadas cartesianas las dos formas del vector son equivalentes. Podemos calcular el producto escalar de dos vectores como el producto matricial de un vector por el traspuesto del otro
y con coordenadas cartesianas las dos formas del vector son equivalentes. Podemos calcular el producto escalar de dos vectores como el producto matricial de un vector por el traspuesto del otro
![\vec{a}\cdot\vec{b} =
\vec{a}\cdot\vec{b}^T=
[a_1, a_2, a_3]
\left[
\begin{array}{c}
b_1 \\ b_2 \\ b_3
\end{array}
\right]
= a_1b_1 + a_2b_2 + a_3b_3 = \sum\limits_{i=1}^3a_ib_i](/wiki/images/math/1/3/c/13cf7d32702efa34c1117e0bbc24123f.png)
Calculamos el producto diádico de dos vectores como el producto matricial del vector traspuesto del primero por el segundo
![\vec{a}\vec{b}
=
\vec{a}^T\vec{b}
=
\left[
\begin{array}{c}
a_1 \\ a_2 \\ a_3
\end{array}
\right]
[b_1, b_2, b_3]
=
\left[
\begin{array}{ccc}
a_1b_1 & a_1b_2 & a_1b_3 \\
a_2b_1 & a_2b_2 & a_2b_3 \\
a_3b_1 & a_3b_2 & a_3b_3
\end{array}
\right]](/wiki/images/math/7/d/4/7d469521d459901451b54689afc31a3d.png)
Es importante observar que no hay un punto entre los dos vectores, como ocurre en el producto escalar. El resultado de la operación es un tensor. Recordemos que la matriz que hemos obtenido es una representación del tensor, pero no el tensor en sí. Si cambiamos el sistema de coordenadas los elementos de la matriz cambian, pero el tensor no.
2.1 Propiedades del producto diádico
- Linealidad
Es lineal respecto a los vectores que lo forman
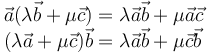
- No es conmutativo
El producto diádico no es conmutativo
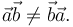
- Traza
La traza de la matriz que representa el producto diádico es el producto escalar de los vectores que lo forman