Entrar Página Discusión Historial Go to the site toolbox

Cilindro desenrrollándose en cuerda vertical, Enero 2018 (G.I.E.R.M.)

De Laplace

Contenido

1 Enunciado

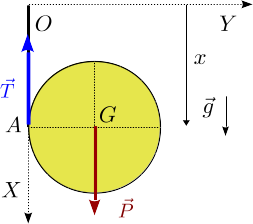
Un disco homogéneo de masa m y radio R se desenrolla bajo la acción de la gravedad sobre una cuerda vertical, como se indica en la figura, de forma que la velocidad del punto de contacto del disco con la cuerda es siempre nula. La cuerda se mantiene siempre vertical. El punto O al que está atada la cuerda es un punto fijo.

  1. Escribe el vector de posición, velocidad y aceleración del centro del disco. ¿Cuál es la relación entre la velocidad del centro del disco y su velocidad de rotación?
  2. En el instante inicial el disco está en reposo con x(0) = 0. Calcula la velocidad del centro del disco en función de su posición.
  3. Calcula la fuerza neta que actúa sobre el disco y la tensión de la cuerda.

2 Solución

2.1 Vectores del centro del disco

Los vectores de posición, velocidad y aceleración del centro del disco son

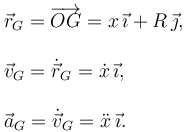
\begin{array}{l} \vec{r}_{G} = \overrightarrow{OG} = x\,\vec{\imath} + R\,\vec{\jmath},\\ \\ \vec{v}_{G} = \dot{\vec{r}}_G = \dot{x}\,\vec{\imath},\\ \\ \vec{a}_{G} = \dot{\vec{v}}_G = \ddot{x}\,\vec{\imath}. \end{array}

La velocidad del punto A del disco es nula en cada instante: 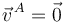\vec{v}^{\,A}=\vec{0}. Usando la ecuación del campo de velocidades del sólido tenemos

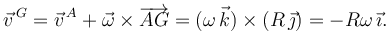
\vec{v}^{\,G} = \vec{v}^{\,A} + \vec{\omega}\times\overrightarrow{AG} = (\omega\,\vec{k})\times(R\,\vec{\jmath}) = -R\omega\,\vec{\imath}.

Comparando con la expresión anterior vemos que

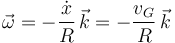
\vec{\omega} = -\dfrac{\dot{x}}{R}\,\vec{k} = -\dfrac{v_G}{R}\,\vec{k}

Vamos a usar 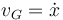v_G=\dot{x}.

2.2 Velocidad del centro en función de la posición

El disco está sometido a dos fuerzas: el peso, que es conservativa, y la fuerza ejercida por la cuerda, que no lo es. Pero esta última no hace trabajo, pues el punto donde se aplica, A, no tiene velocidad. Entonces se conserva la energía mecánica.

La energía mecánica del disco es la suma de su energía cinética y su energía potencial. La energía cinética tiene dos componentes: la de traslación del centro de masas y la de rotación alrededor del centro de masas.

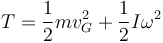
T = \dfrac{1}{2}mv_G^2 + \dfrac{1}{2}I\omega^2

Aquí, I es el momento de inercia del disco respecto a un eje perpendicular a él que pasa por su centro. Usando el apartado anterior tenemos

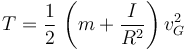
T = \dfrac{1}{2}\,\left(m+\dfrac{I}{R^2}\right)v_G^2

La energía potencial es la debida a la gravedad. Tomando como referencia la altura x = 0 tenemos

U = Ug = − mgx.

El signo es negativo pues la coordenada x crece hacia abajo. Así pues, la energía mecánica en cualquier instante es

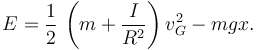
E = \dfrac{1}{2}\,\left(m+\dfrac{I}{R^2}\right)v_G^2 - mgx.

En el instante inicial el disco está en reposo y x = 0. por tanto

E(t = 0) = 0.

Como se conserva tenemos

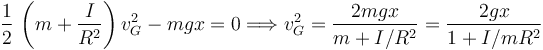
\dfrac{1}{2}\,\left(m+\dfrac{I}{R^2}\right)v_G^2 - mgx = 0 \Longrightarrow v_G^2 = \dfrac{2mgx}{m+I/R^2} = \dfrac{2gx}{1+I/mR^2}

Para un disco I = mR2 / 2, entonces

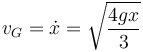
v_G = \dot{x} = \sqrt{\dfrac{4gx}{3}}

2.3 Tensión en la cuerda

El Teorema del Centro de Masas aplicado sobre el disco nos da

m\vec{a}_G = \vec{P} + \vec{T} \Longrightarrow \vec{T} = m\vec{a}_G - \vec{P}

El peso es

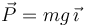
\vec{P} = mg\,\vec{\imath}

La aceleración es

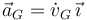
\vec{a}_G = \dot{v}_G\,\vec{\imath}

Del apartado anterior, usando la regla de la cadena

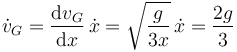
\dot{v}_G = \dfrac{\mathrm{d}v_G}{\mathrm{d}x}\,\dot{x} = \sqrt{\dfrac{g}{3x}}\,\dot{x} = \dfrac{2g}{3}

Es decir, el centro del disco realiza un movimiento uniformemente acelerado con aceleración

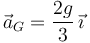
\vec{a}_G = \dfrac{2g}{3}\,\vec{\imath}

Entonces la tensión de la cuerda es

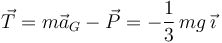
\vec{T} = m\vec{a}_G - \vec{P} = -\dfrac{1}{3}\,mg\,\vec{\imath}

La fuerza neta sobre el disco es

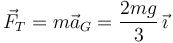
\vec{F}_T = m\vec{a}_G = \dfrac{2mg}{3}\,\vec{\imath}

2.4 Resolución alternativa

El problema puede resolverse también usando los Teoremas del Centro de Masas y del Momento Cinético aplicados al disco.

La figura del apartado anterior muestra el diagrama de cuerpo libre del disco. El Teorema del Centro de Masas nos dice

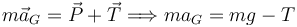
m\vec{a}_G = \vec{P} + \vec{T} \Longrightarrow ma_G = mg - T

El Teorema del Momento Cinético aplicado en el centro del disco nos da

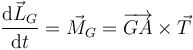
\dfrac{\mathrm{d}\vec{L}_G}{\mathrm{d}t} = \vec{M}_G = \overrightarrow{GA}\times\vec{T}

El momento cinético es

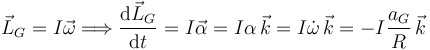
\vec{L}_G = I\vec{\omega} \Longrightarrow \dfrac{\mathrm{d}\vec{L}_G}{\mathrm{d}t} = I\vec{\alpha} = I\alpha\,\vec{k} = I\dot{\omega}\,\vec{k} = -I\dfrac{a_G}{R}\,\vec{k}

El momento es

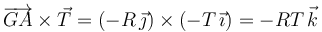
\overrightarrow{GA}\times\vec{T} = (-R\,\vec{\jmath})\times(-T\,\vec{\imath}) = -RT\,\vec{k}

Entonces

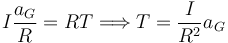
I\dfrac{a_G}{R} = RT \Longrightarrow T = \dfrac{I}{R^2}a_G

Sustituyendo en la ecuación obtenida del Teorema del Centro de Masas obtenemos

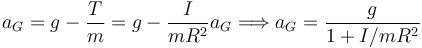
a_G = g - \dfrac{T}{m} = g - \dfrac{I}{mR^2}a_G \Longrightarrow a_G = \dfrac{g}{1+I/mR^2}

Sustituyendo el valor de I reobtenemos la solución anterior para la aceleración.

Obtenido de "http://tesla.us.es/wiki/index.php/Cilindro_desenrroll%C3%A1ndose_en_cuerda_vertical,_Enero_2018_(G.I.E.R.M.)"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Aviso legal - Acerca de Laplace