Los gases ideales (GIE)

De Laplace

Revisión a fecha de 17:07 7 feb 2018; Antonio (Discusión | contribuciones)

(dif) ← Revisión anterior | Revisión actual (dif) | Revisión siguiente → (dif)

1 Ecuación general

Combinando la ley de Charles con la de Boyle obtenemos, para un sistema cerrado en el que la masa de gas permanece constante,

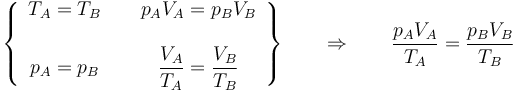
$\left\{\begin{array}{ccc}T_A=T_B&\ & p_AV_A=p_BV_B \\ && \\ p_A=p_B & \ & \displaystyle\frac{V_A}{T_A}=\displaystyle \frac{V_B}{T_B}\end{array}\right\}\qquad\Rightarrow\qquad \frac{p_AV_A}{T_A}=\frac{p_BV_B}{T_B}$

o, equivalentemente,

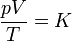
$\frac{pV}{T}=K$

siendo K una constante específica para cada muestra de gas y que no depende ni de la presión, ni del volumen, ni de la temperatura. Puesto que el primer miembro es una cantidad extensiva (el volumen es proporcional a la masa), el segundo miembro también debe serlo, por lo que puede escribirse en la forma

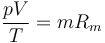
$\frac{pV}{T}=mR_m$

siendo $R m$ una constante diferente para cada gas (constante del gas).

Una tabla de valores, tomada de Engineering toolbox y de Pipe Flow calculations sería la siguiente:

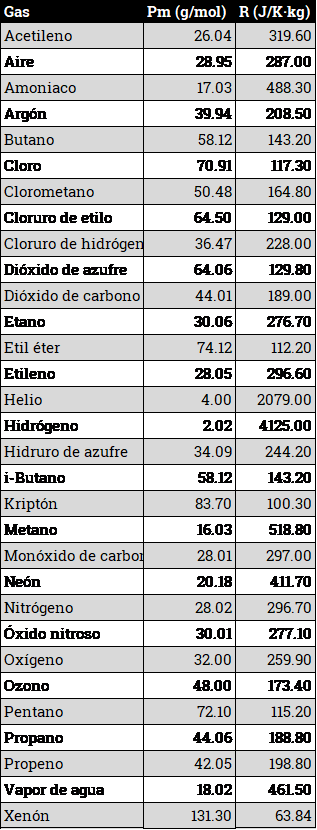
1.1 Gases puros

Si a partir de la tabla anterior se representa la constante de cada gas en función del peso molecular, podemos ver, mediante una escala logarítmica, que esa constante es, muy aproximadamente, inversamente proporcional al peso molecular

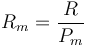
$R_m=\frac{R}{P_m}$

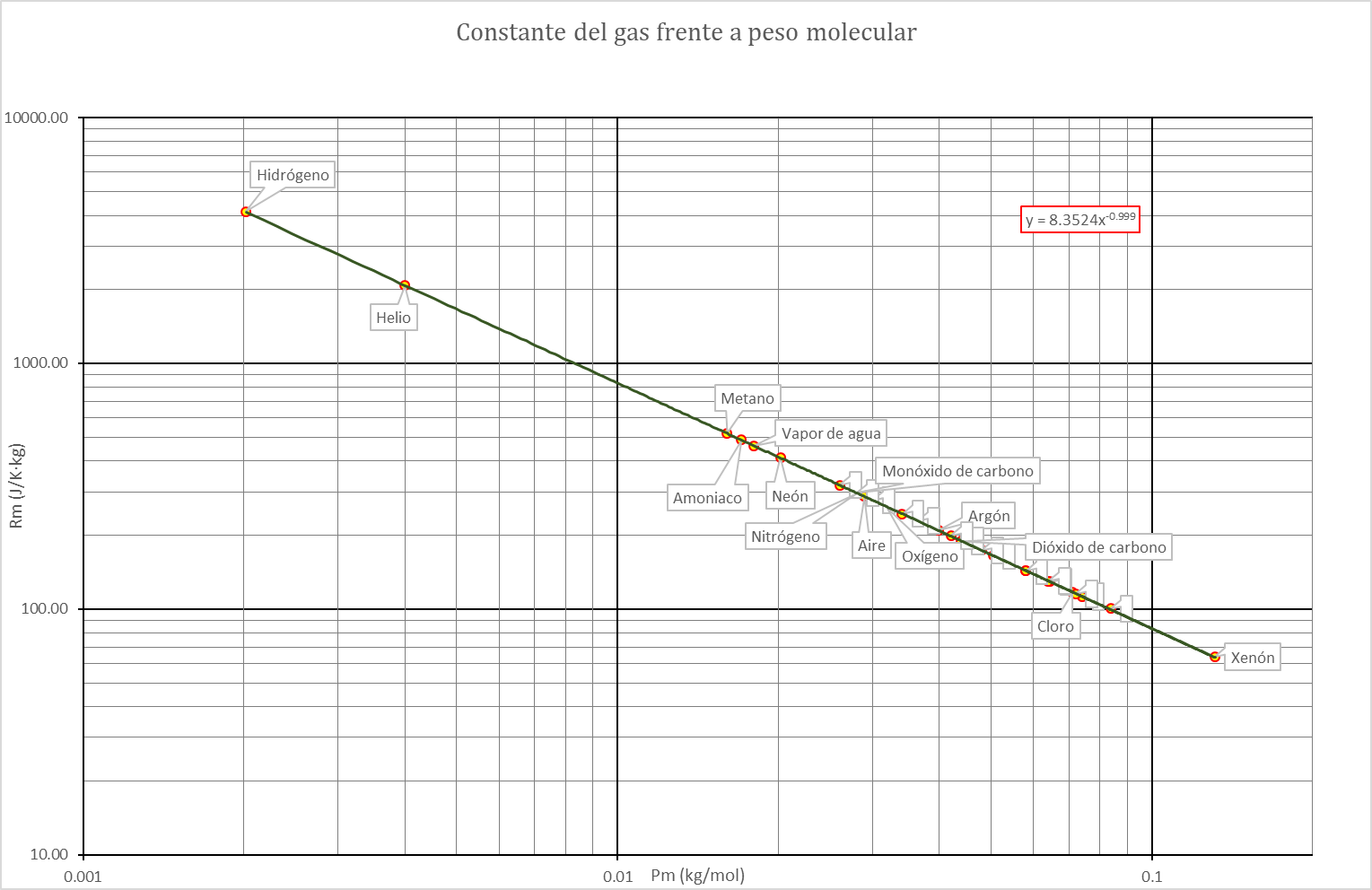
Para un gas puro, constituido por un solo tipo de moléculas, la ley de los gases ideales puede escribirse en función del número de moles

$n=\frac{m}{P_m}\qquad\Rightarrow\qquad \frac{pV}{T}= n P_mR_m$

siendo $P m$ el peso molecular. Se encuentra experimentalmente que el producto

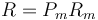
$R=P_mR_m\,$

es prácticamente independiente del gas de que se trate. Por ello, a la constante $R$ se la denomina constante universal de los gases ideales. De esta forma, queda la ecuación general

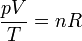
$\frac{pV}{T}=nR$

El valor de $R$ en el SI es

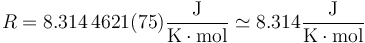
$R = 8.314\,4621(75)\frac{\mathrm{J}}{\mathrm{K}\cdot\mathrm{mol}}\simeq 8.314\frac{\mathrm{J}}{\mathrm{K}\cdot\mathrm{mol}}$

Esta ecuación de estado suele escribirse en la forma

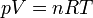
$pV = nRT\,$

1.2 Mezclas ideales de gases ideales. El aire seco

Las mezclas de gases, como el aire seco (sin vapor de agua), no son sustancias puras, sino que combinan diferentes tipos de moléculas. Por ello, aunque cumplen la ley de los gases ideales

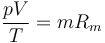
$\frac{pV}{T}=mR_m$

con

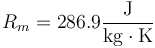
$R_m = 286.9\frac{\mathrm{J}}{\mathrm{kg}\cdot\mathrm{K}}$

para el aire seco, no es trivial pasar esta expresión a número de moles, ya que ¿qué es un mol de aire? No podemos multiplicar la constante por el peso molecular del aire, pues no está definido en principio (¿es el del nitrógeno? ¿el del oxígeno? ¿cómo se combinan?). De hecho, podemos emplearla para definir un peso molecular efectivo

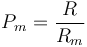
$P_m=\frac{R}{R_m}$

que nos da, para el aire seco,

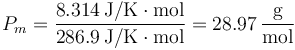
$P_m=\frac{8.314\,\mathrm{J}/\mathrm{K}\cdot\mathrm{mol}}{286.9\,\mathrm{J}/\mathrm{K}\cdot\mathrm{mol}}=28.97\,\frac{\mathrm{g}}{\mathrm{mol}}$

Ahora bien, podemos llegar al peso molecular efectivo de otra forma.

En una mezcla ideal de gases ideales, no solo se comporta idealmente cada gas por separado, sino que no interactúan entre sí. En ese caso, cada molécula se mueve independientemente y los choques que puedan tener con las paredes no dependen del resto de sustancias. Por tanto la presión resultante es la suma de las presiones parciales, que son las que producirían los distintos gases si estuvieran solos en el recipiente

$p=\sum_i p_i\,\qquad\qquad p_i = \frac{n_i R T}{V}$

Como cada gas es ideal y la temperatura de cada uno y el volumen que ocupa es el mismo para todos

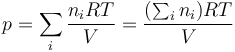
$p=\sum_i \frac{n_i R T}{V}=\frac{(\sum_i n_i)RT}{V}$

Comparando con la ecuación de los gases ideales para una sustancia pura, podemos definir el número de moles de aire como

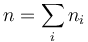
$n=\sum_i n_i\,$

Por otro lado, la masa total del aire es la suma de las de los gases constituyentes

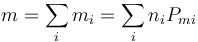
$m=\sum_i m_i = \sum_i n_i P_{mi}\,$

lo que nos permite definir el peso molecular del aire como

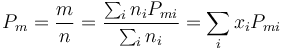
$P_m=\frac{m}{n}=\frac{\sum_i n_iP_{mi}}{\sum_i n_i}=\sum_i x_iP_{mi}$

siendo $x i$ la fracción molar del gas i

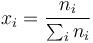
$x_i=\frac{n_i}{\sum_i n_i}$

Aplicando esto al caso del aire seco, que tiene una fracción molar de 78.1% de N2, 20.9% de O2 y 1.0% de Ar (más otros gases en fracciones menores) resulta un peso molecular efectivo

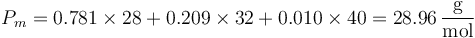
$P_m = 0.781\times 28+0.209\times 32 + 0.010\times 40 = 28.96\,\frac{\mathrm{g}}{\mathrm{mol}}$

de acuerdo con el otro cálculo.

Los gases ideales (GIE)

De Laplace

1 Ecuación general

1.1 Gases puros

1.2 Mezclas ideales de gases ideales. El aire seco

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES