Dos partículas unidas por un hilo que cuelga
De Laplace
Contenido |
1 Enunciado
Dos partículas de masas m1 y m2 están unidas por un hilo ideal (inextensible y sin masa) de longitud b. La partícula 1 se encuentra sobre la superficie horizontal z = 0 mientras que el hilo pasa por un orificio situado en el origen O y la masa m2 pende verticalmente.
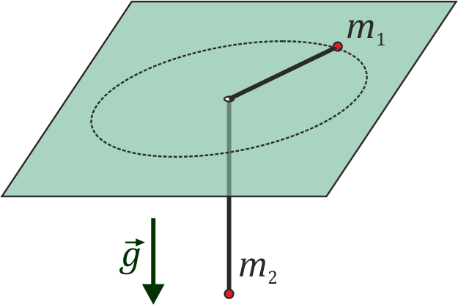
- ¿Con qué rapidez debe moverse la masa 1 describiendo circunferencias si la masa 2 se mantiene en equilibrio en una posición z2 = − h? ¿Cuál es la tensión del hilo en ese caso?
- Suponga que se aplica una fuerza vertical
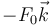 sobre la masa 2, ¿cuál es la nueva posición de equilibrio de la masa 2?
sobre la masa 2, ¿cuál es la nueva posición de equilibrio de la masa 2?
- Si la fuerza F0 se aplica en t = 0 estando las masas inicialmente en la situación del apartado 1, ¿cuál es la ecuación de movimiento para cada masa?
- Indique dos constantes de movimiento para este problema
2 Movimiento circular
Las dos partículas están sometidas al vínculo
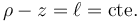
por estar unidas por un hilo ideal inextensible.
Para que la partícula 1 describa órbitas circulares debe estar sometida a una fuerza centrípeta constante, que en este caso es ejercida por la tensión del hilo
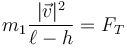
siendo 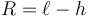 el radio de la circunferencia. Esta misma tensión actúa sobre la masa 2, equilibrando al peso, ya que la esta masa no se mueve
el radio de la circunferencia. Esta misma tensión actúa sobre la masa 2, equilibrando al peso, ya que la esta masa no se mueve

y por tanto

3 Caso con fuerza aplicada
Si se aplica una fuerza F0 a la masa que cuelga, el nuevo estado de equilibrio se obtiene simplemente sustituyendo el peso real por uno efectivo. Entonces, si la rapidez siguiera sioendo la misma, el hilo se acortaría según la ley
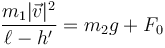
Si sustituimos la rapidez del apartado anterior nos queda
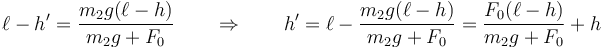
Sin ambargo, no es esto lo que ocurre. Como veremos, el momento cinético del sistema respecto a O se conserva, por lo que para movimientos circulares
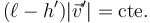
es decir, que si se acorta el hilo aumenta la rapidez. Entonces la nueva longitud de equilibrio sale del sistema

Esto nos da
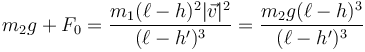
y por tanto, la verdadera longitud de equilibrio con la carga extra es
![\ell- h'=(\ell-h)\sqrt[3]{\frac{m_2g}{m_2g+F_0}}](/wiki/images/math/9/0/6/9069acfe2abdd4290b5a7ed454394769.png)
4 Ecuaciones de movimiento
No obstante lo anterior, cuando la partícula 1 se encuentra ya describiendo una órbita circular, el sistema no pasa al nuevo estado de equilibrio. En su lugar, lo que ocurre es que la fuerza extra empuja a la masa 2 hacia abajo y la 1 se ve acercada hacia el centro, pero al hacerlo empieza a girar más rápido en torno al origen.
Las ecuaciones de movimiento para la partícula las podemos escribir en coordenadas polares

y para la partícula 2

Introduciendo aquí la ecuación del vínculo y sumando con la primera ecuación nos queda
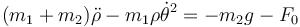
De la ecuación de movimiento acimutal podemos obtener una constante de movimiento. Si multiplicamos por ρ queda
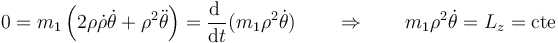
Esta constante se puede sustituir en la ecuación radial y nos queda finalmente una ecuación para esta coordenada
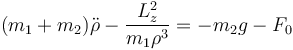
5 Constantes de movimiento
En este sistema tenemos dos constantes de movimiento no triviales.
5.1 El momento cinético respecto a O
Dado que todas las fuerzas actúan sobre rectas que pasan por O, el momento cinético respecto a este punto es constante. Este momento es igual a

que es justo la constante que acabamos de determinar.
5.2 Energía mecánica
El sistema es conservativo, por lo que
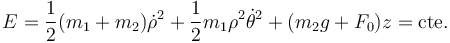
6 Caso de perturbación débil
Supongamos que la fuerza F0 es pequeña comparada con el peso, de forma que las partículas se ven poco afectadas por esta fuerza extra. Nos preguntamos entonces por el movimiento que siguen las dos en esta aproximación.
Tenemos la ecuación de movimiento
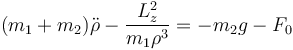
Suponemos un estado inicial en el que
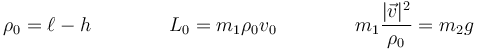
Si suponemos una pequeña perturbación respecto a este estado

podemos efectuar el desarrollo de Taylor de esta ecuación alrededor de ρ0 y el resultado es la ecuación aproximada
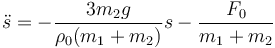
Esta es una ecuación del tipo de las del oscilador armónico, con solución de la forma
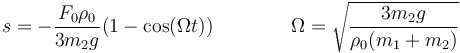
donde hemos aplicado las condiciones iniciales

Este resultado nos dice que las masas realizan un movimiento oscilatorio alrededor de la posición de equilibrio. la que cuelga sube y baja y la del plano hace una circunferencia deformada por un vaivén en el que se acerca y se aleja del centro.





