Composición general de movimientos (CMR)
De Laplace
Contenido |
1 Generalización de las fórmulas
Las fórmulas de composición de velocidades pueden extenderse a cualquier terna de sólidos, de manera que tenemos las relaciones para la velocidad angular
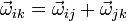
y para la velocidad lineal instantánea de un punto O
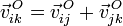
Si en vez de tres sólidos tenemos una cadena de sólidos 1,2,...,n, por ejemplo, en un brazo articulado con diferentes tramos compuesta por cuatro o más sólidos y lo que nos interesa es el movimiento absoluto final del sólido n respecto al sólido 1, su velocidad angular será la suma de las de los diferentes movimientos relativos
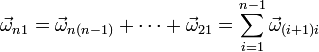
y la velocidad lineal de un punto O,
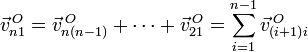
La velocidad de cualquier otro punto puede hallarse bien empleando esta misma fórmula, esto es, hallando la velocidad de P en cada uno de los movimientos relativos y luego sumando los resultados, o bien empleando la expresión del campo de velocidades de un sólido
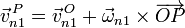
En particular, si los movimientos relativos son todos rotaciones puras y los puntos O1, O2,... son puntos de los sucesivos ejes instantáneos de rotación, la velocidad lineal del punto P será
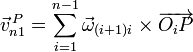
2 Composiciones equivalentes
El resultado anterior indica que existen diferentes, infinitas de hecho, composiciones de movimientos que producen el mismo movimiento absoluto final. Desde el punto de vista cinemático, es lo mismo empujar una caja sobre el suelo, que montarla sobre rodillos para trasladarla.
Definimos entonces como equivalentes dos composiciones de N movimientos si producen el mismo movimiento absoluto. Es claro que esta relación es de equivalencia (verifica las propiedades reflexiva, simétrica y transitiva).
Matemáticamente, las condiciones para que dos composiciones de movimientos sean equivalentes son:
- Misma velocidad angular neta
- La velocidad angular neta, suma de las velocidades angulares relativas, debe ser la misma en las dos composiciones
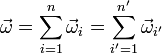
- donde abreviamos la notación usando un solo subíndice para indicar la i-ésima velocidad angular. A la velocidad angular neta, que es un vector libre, como cada uno de los sumandos, se la denomina la resultante o vector rotación total del sistema.
- Misma velocidad de un punto
- Para un cierto punto O, la velocidad lineal resultante en ambas composiciones debe ser la misma
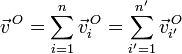
Obsérvese que, si dos composiciones de movimientos conducen a una misma velocidad angular neta y a una misma velocidad en cierto punto O (igual reducción cinemática en O), esto implica que ambas composiciones conducen a idénticos campos de velocidades.
No es esta la única forma de establecer la equivalencia. Puesto que el campo de velocidades de un movimiento rígido se puede caracterizar de formas alternativas, cada una de ellas puede usarse para establecer la equivalencia. Así podemos requerir:
- Dos composiciones son equivalentes si producen la misma velocidad lineal en tres puntos dados (no alineados).
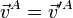
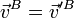
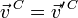
El conjunto de todas las composiciones equivalentes forma una clase de equivalencia, que puede ser representada por uno cualquiera de sus elementos. Cuando este representante es un movimiento rígido elemental caracterizado por una velocidad angular y la velocidad lineal de un punto O se dice que hemos reducido la composición en el punto O.
En particular la reducción se dice canónica si el punto O pertenece al EIRMD.
De acuerdo con los posibles movimientos de un sólido obtenemos que los posibles resultados de las composiciones de N movimientos son:
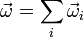
| 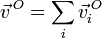
| Estado |
|---|---|---|
| 
| Reposo |
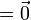
| 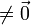
| Traslación |
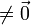
| 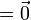
| Rotación |
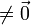
| 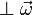
| Rotación |
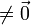
| 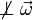
| Helicoidal |
3 Casos particulares
3.1 Composición de dos o más traslaciones
La composición de cualquier número de traslaciones es otra traslación (incluyendo el reposo como caso particular)
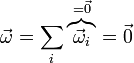
La velocidad de cualquiera de los puntos del sistema será la suma de las de las traslaciones individuales
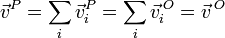
En particular la composición de dos traslaciones iguales y opuestas es un estado de reposo.
La composición de N traslaciones es una traslación. Sin embargo, la composición de N rotaciones no es, en general, igual a una rotación. De hecho, como veremos, puede producir cualquier movimiento.
3.2 Par de rotaciones opuestas
Consideremos la composición de dos rotaciones puras cuyas velocidades angulares son iguales y opuestas
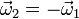
y cuyos ejes instantáneos de rotación, necesariamente paralelos, están separados una distancia d. La velocidad angular resultante de estas dos rotaciones es nula
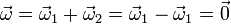
Por tanto el movimiento resultante es uno de traslación o de reposo. Si O1 y O2 son sendos puntos en los respectivos ejes instantáneos de rotación, la velocidad de cualquier otro punto P es
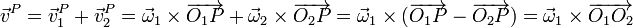
Este resultado es independiente del punto P, pero no es nulo en general. Esto quiere decir que el resultado de dos rotaciones opuestas sobre ejes paralelos es una traslación con velocidad
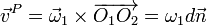
con módulo
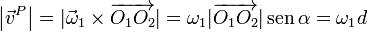
y dirección la normal al plano formado por los dos ejes instantáneos de rotación.
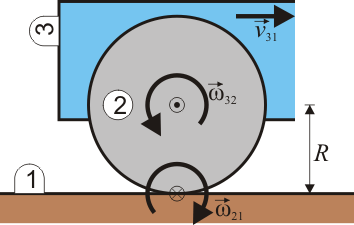
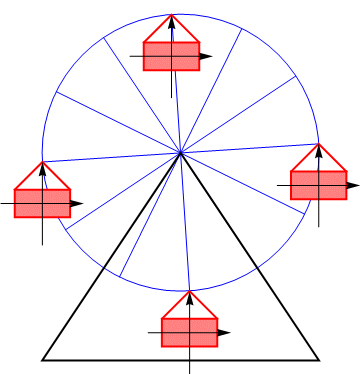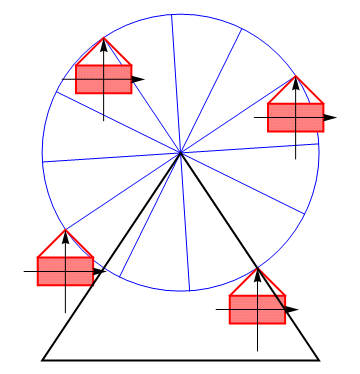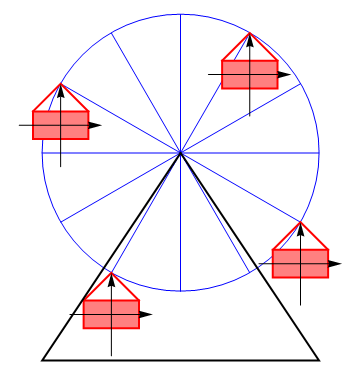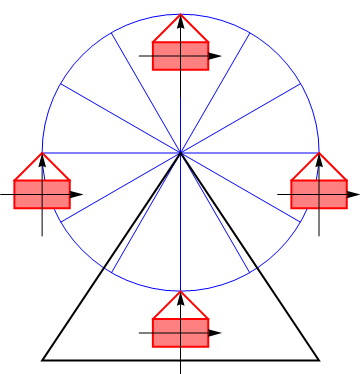
Ejemplos sencillos de esta composición lo tenemos en el caso de un vehículo que avanza sobre ruedas. Si el cuerpo del vehículo es el sólido 3, el suelo el sólido 1, y una rueda el sólido intermedio 2, ésta gira con la misma velocidad angular respecto al eje de la rueda que respecto a la línea de contacto con el suelo
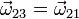

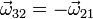

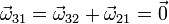
La celeridad de traslación del cuerpo del vehículo respecto al suelo será
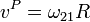
con R el radio de la rueda, que es la distancia entre los dos ejes instantáneos de rotación.
El mismo principio se aplica a la traslación de las vagonetas de una noria, que mantienen su orientación a partir de la combinación de dos rotaciones opuestas.
Jugando con los valores de  y de d podemos obtener cualquier valor para la velocidad de traslación. Por tanto:
y de d podemos obtener cualquier valor para la velocidad de traslación. Por tanto:
- Toda traslación es equivalente a un par de rotaciones opuestas sobre ejes paralelos.
y, puesto que un movimiento rígido es siempre equivalente a una traslación más una rotación llegamos a que:
- Todo movimiento rígido es equivalente a una composición de rotaciones puras.
Por tanto, el estudio de las composiciones de movimientos puede reducirse a considerar un conjunto de rotaciones alrededor de ciertos ejes instantáneos de rotación. De hecho, eligiendo adecuadamente los ejes, todo movimiento rígido puede escribirse como composición de solo dos rotaciones.
3.3 Caso de rotaciones concurrentes. Teorema de Varignon
Consideremos ahora el caso de N rotaciones puras cuyos ejes instantáneos de rotación pasan todos por el mismo punto O. El resultado de la composición tendrá una velocidad angular
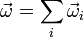
mientras que la velocidad del punto O será nula
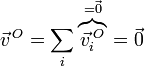
Por tanto, la combinación de N rotaciones a través de ejes concurrentes (que pasan por un punto común), es otra rotación a través de un eje que pasa por el mismo punto y cuya velocidad angular es la suma de las velocidades angulares individuales. Este es el conocido como teorema de Varignon.
Un caso particular ilustrativo es el movimiento de una peonza, que puede verse como una composición de dos rotaciones: una alrededor de su eje (llamada movimiento de rotación), compuesta con una rotación de este eje alrededor de un eje vertical (llamada movimiento de precesión). Si además este eje se bambolea arriba y abajo (lo cual puede verse como una rotación alrededor de un eje horizontal), se dice que tiene además un movimiento de nutación.