Composición de dos movimientos (CMR)
De Laplace
Contenido |
1 Composición de velocidades
Una vez que disponemos de la fórmula de Poisson, podemos aplicarla para relacionar la velocidad de un punto, medida por dos observadores diferentes.
Supongamos un punto P, que se mueve con el sólido móvil 2, tal que su vector de posición respecto al origen O1 de un sistema fijo 1 es
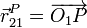
y respecto al origen O de un sólido intermedio 0 es
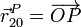
Estos dos vectores se relacionan por
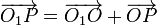

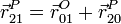
Derivando aquí respecto al tiempo en el sistema 1 llegamos a la relación
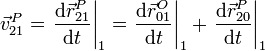
El primero de los dos términos es la velocidad del punto O, medida en el sistema 1.
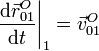
Para el segundo, relacionamos esta derivada con la medida en el sólido 0
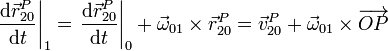
Sumando las dos contribuciones
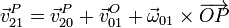
Si aquí sustituimos el campo de velocidades del sólido 0, la velocidad se reduce a
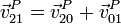
esto es: la velocidad del punto P del sólido móvil, medida por un observador ligado al sólido “1” (que tomamos como fijo o de referencia) es la suma de la medida por uno ligado al sólido intermedio “0” más la que tendría el punto P, si perteneciera al sólido intermedio “0”, medida en el sistema fijo.
Este resultado es aplicable a cualquier terna de sólidos. En general
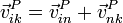
No hay nada de especial que convierta a 0 en el sólido intermedio y a 1 en fijo; del mismo modo tenemos
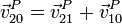
donde se han intercambiado sus papeles. Comparando esta expresión con la anterior obtenemos que
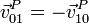
Hay que destacar que la expresión de la velocidad como suma de velocidades es una relación entre valores instantáneos de las diferentes cantidades, no como funciones del tiempo. Por tanto, no puede derivarse respecto al tiempo para hallar las aceleraciones. La razón es la siguiente: en la expresión aparece la velocidad del punto P del sólido 0, pero el punto P no es siempre el mismo punto material en el sólido 0, sino aquel que en cada instante coincide con el punto P del sólido 2 (que sí es un punto material), esto quiere decir que en el instante t empleamos la velocidad de un punto P, pero en el instante t + dt empleamos la velocidad de otro punto P diferente, y la diferencia de estas dos velocidades no da la aceleración de ninguno de los dos.
La expresión en términos de la velocidad de O y la velocidad angular, en cambio, si puede derivarse respecto al tiempo, ya que el punto O del sólido 0 si está perfectamente definido y se puede seguir su movimiento en el tiempo.
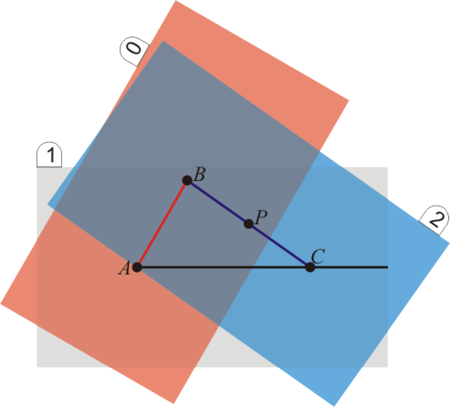
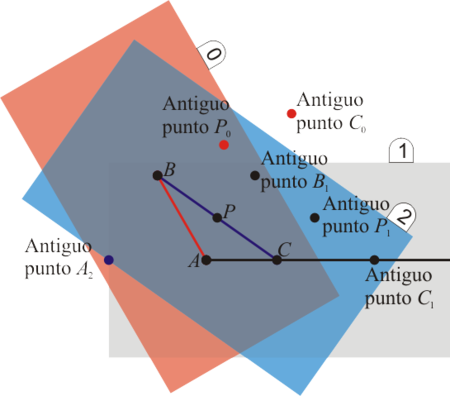
Una consecuencia de la ecuación anterior, y que parece ir contra el sentido común, es la siguiente. Supongamos que tenemos dos observadores A y B, pertenecientes a sólidos 1 y 2, respectivamente. En general, no se cumple que la velocidad de A medida por B sea opuesta a la de B medida por A
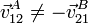
En este problema se analiza un ejemplo que muestra distintas variantes de esta desigualdad.
2 Composición de velocidades angulares
Una vez que tenemos la relación entre velocidades lineales, podemos hallar la de velocidades angulares.
Partimos de la ley de composición de velocidades. Tenemos que, en un instante dado, y para cualquier punto P
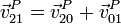
Restando esta expresión de la correspondiente a otro punto O nos queda la relación entre velocidades relativas
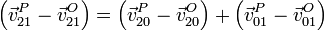
En esta expresión los tres movimientos son rígidos, por lo que verifican
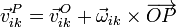
lo que nos da la relación
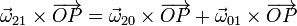
Puesto que esta relación debe cumplirse para todos los pares de puntos, la única posibilidad es que
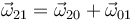
A diferencia de la ecuación para las velocidades, esta relación sí puede derivarse respecto al tiempo. La razón es que la velocidad angular es un invariante, no depende de la posición de ningún punto en concreto, por lo que desaparece el problema de si el punto P en cada instante es el mismo o no.
3 Composición de aceleraciones. Teorema de Coriolis
Podemos relacionar las aceleraciones medidas por dos observadores a partir de la expresión
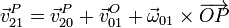
Derivando respecto al tiempo en el sistema 1 obtenemos, para cada uno de los términos
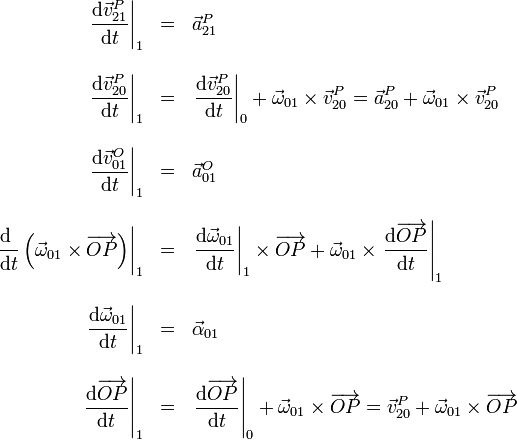
Sustituyendo todo esto obtenemos
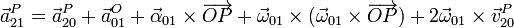
Agrupando términos con ayuda de la expresión del campo de aceleraciones de un sólido obtenemos finalmente
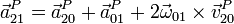
Este es el conocido como Teorema de Coriolis. Vemos que, a diferencia de la velocidad, la aceleración del movimiento absoluto no es la suma de la del movimiento relativo más la del de arrastre.
En el caso particular de que el sólido 2 y el 1 sean el mismo obtenemos
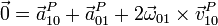

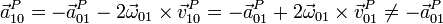
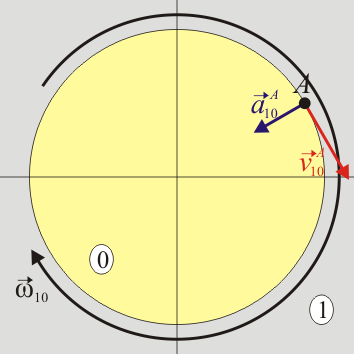
Podemos ilustrar el que no resulten aceleraciones iguales y opuestas con un ejemplo sencilo. Consideremos una plataforma “0” que gira con velocidad angular constante respecto al suelo, considerado como sólido “1”. Sea un punto A de la plataforma. Para un observador situado en el suelo “1”, este punto A está describiendo un movimiento circular uniforme en torno al eje de la plataforma. Por tanto su aceleración, 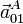 será radial y hacia adentro.
será radial y hacia adentro.
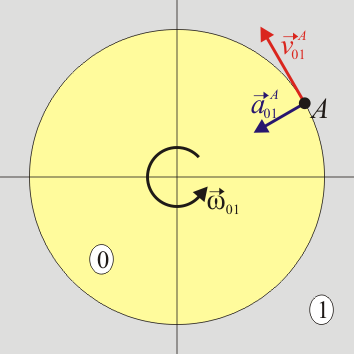
| 
|
| Desde el suelo | Desde la plataforma |
|---|
Desde el punto de vista del sólido “0”, en cambio, es el suelo el que gira con velocidad angular constante en sentido contrario. Para este observador un punto A del suelo también está describiendo un movimiento circular uniforme. Por tanto, la aceleración de este punto A del suelo, 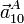 , también será radial y hacia adentro. Esto es, que para este caso concreto
, también será radial y hacia adentro. Esto es, que para este caso concreto
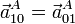
Resulta una velocidad igual en módulo y opuesta, una velocidad angular igual en módulo y opuesta, pero una aceleración que no es igual en módulo y opuesta, sino igual a secas. En la fórmula de composición de aceleraciones, el término de Coriolis en este caso es exactamente igual en módulo al doble del primer sumando y con sentido opuesto
4 Composición de aceleraciones angulares
La ley para la composición de aceleraciones angulares la obtenemos derivando la ley de composición de velocidades angulares
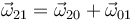
Derivando cada término resulta
- Derivada de la velocidad angular absoluta
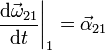
- Derivada de la velocidad angular relativa
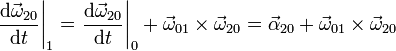
- Derivada de la velocidad angular de arrastre
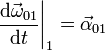
Combinando todos estos términos:
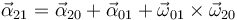
En el caso particular de que el sólido 2 y el 1 sean el mismo nos queda
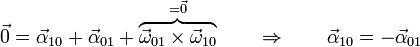
esto es, la aceleración angular sí es antisimétrica, a diferencia de lo que ocurre con la aceleración lineal.





