Campo de aceleraciones de un sólido

De Laplace

Revisión a fecha de 16:46 2 nov 2017; Antonio (Discusión | contribuciones)

(dif) ← Revisión anterior | Revisión actual (dif) | Revisión siguiente → (dif)

Contenido

1 Introducción
2 Aceleración de un punto
3 Campo de aceleraciones
- 3.1 Caso de movimiento de O conocido
- 3.2 Caso de campo de velocidades conocido

1 Introducción

El cálculo de la aceleración de una partícula de un sólido a partir del campo de velocidades no es trivial, ya que no basta con derivar respecto al tiempo. La aceleración es la derivada temporal de la velocidad de P, no de la velocidad en P.

¿Qué quiere decir esto? Supongamos que conocemos la velocidad en el punto P (del sistema fijo, no del móvil) en todo instante, 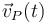$\vec{v}_P(t)$ . La derivada de esta función respecto al tiempo no coincide con la aceleración de P porque la partícula material que se halla en P es distinta en cada instante; no estaríamos restando la velocidad de la misma partícula entre dos instantes sucesivos. Matemáticamente estamos hallando la derivada parcial respecto al tiempo, ya que consideramos las coordenadas x, y y z como constantes.

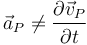
$\vec{a}_P\neq\frac{\partial \vec{v}_P}{\partial t}$

2 Aceleración de un punto

Para hallar la aceleración de un punto P pueden ocurrir dos casos:

Que conozcamos la velocidad en todo instante de un punto material, estacionario en el sistema ligado. Por ejemplo, podemos saber cómo se mueve el centro de masas del sólido, o saber que el sólido tiene un punto fijo, como ocurre con una peoza.
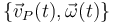
Que conozcamos la reducción cinemática en todo instante, es decir que conozcamos la velocidad angular y la velocidad lineal en un punto P, estacionario en el sistema fijo, $\{\vec{v}_P(t),\vec{\omega}(t)\}$

En el primer caso, la aceleración del punto P se calcula como la de una partícula individual, derivando la velocidad respecto al tiempo.

Si, en cambio, conocemos la velocidad en el sistema fijo en todo instante, debemos calcular el incremento de la velocidad de la partícula de P, teniendo en cuenta que esta se mueve, pasando de P a P' con velocidad 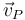$\vec{v}_P$

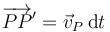
$\overrightarrow{PP}^\prime=\vec{v}_P\,\mathrm{d}t$

de manera que la aceleración de P se calcula como

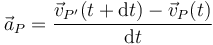
$\vec{a}_P=\frac{\vec{v}_{P'}(t+\mathrm{d}t)-\vec{v}_P(t)}{\mathrm{d}t}$

Aplicamos aquí la expresión del campo de velocidades

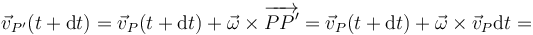
$\vec{v}_{P'}(t+\mathrm{d}t)=\vec{v}_P(t+\mathrm{d}t)+\vec{\omega}\times \overrightarrow{PP^\prime}=\vec{v}_P(t+\mathrm{d}t)+\vec{\omega}\times \vec{v}_P\mathrm{d}t=$

y nos queda la expresión para la aceleración

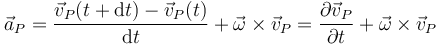
$\vec{a}_P=\frac{\vec{v}_P(t+\mathrm{d}t)-\vec{v}_P(t)}{\mathrm{d}t}+\vec{\omega}\times\vec{v}_P=\frac{\partial \vec{v}_P}{\partial t}+\vec{\omega}\times\vec{v}_P$

Vemos que si el sólido está efectuando una traslación (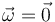 $\vec{\omega}=\vec{0}$ ) o el punto pertenece al EIRMD ( 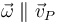$\vec{\omega}\parallel\vec{v}_P$ ) la aceleración sí coincide con la derivada parcial de la velocidad con respecto al tiempo. La misma ecuación se cumple para el punto de referencia O

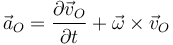
$\vec{a}_O=\frac{\partial \vec{v}_O}{\partial t}+\vec{\omega}\times\vec{v}_O$

3 Campo de aceleraciones

Una vez que tenemos la aceleración de un punto, bien porque sabemos cómo se mueve por el espacio con el tiempo, bien porque podemos calcularla a partir del campo de velocidades, nos planteamos cuánto vale la aceleración en el resto de puntos del sólido.

3.1 Caso de movimiento de O conocido

Si el punto de referencia está identificado y sabemos cómo se mueve (por ejemplo, es el centro de masas) para el resto de puntos podemos aplicar la fórmula de Poisson que relaciona las derivadas en el sistema fijo y el ligado. Dada una expresión vectorial en el sistema ligado

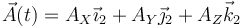
$\vec{A}(t)=A_X\vec{\imath}_2+A_Y\vec{\jmath}_2+A_Z\vec{k}_2$

podemos derivarla respecto al tiempo en el sistema fijo

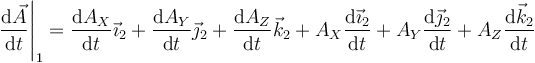
$\left.\frac{\mathrm{d}\vec{A}}{\mathrm{d}t}\right|_1 = \frac{\mathrm{d}A_X}{\mathrm{d}t}\vec{\imath}_2+\frac{\mathrm{d}A_Y}{\mathrm{d}t}\vec{\jmath}_2+\frac{\mathrm{d}A_Z}{\mathrm{d}t}\vec{k}_2+A_X\frac{\mathrm{d}\vec{\imath}_2}{\mathrm{d}t}+A_Y\frac{\mathrm{d}\vec{\jmath}_2}{\mathrm{d}t}+A_Z\frac{\mathrm{d}\vec{k}_2}{\mathrm{d}t}$

Los primeros tres términos representan la derivada respecto al tiempo tal como se ve en el sistema ligado (en en cual la base 2 es estacionaria) y los tres últimos pueden hallarse por las fórmulas de Poisson. Esto nos da

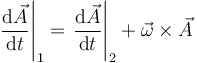
$\left.\frac{\mathrm{d}\vec{A}}{\mathrm{d}t}\right|_1 = \left.\frac{\mathrm{d}\vec{A}}{\mathrm{d}t}\right|_2+\vec{\omega}\times\vec{A}$

Si aplicamos esta fórmula a la velocidad de P, derivando respecto al tiempo en la expresión del campo de velocidades obtenemos la aceleración de punto P

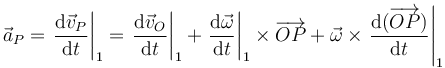
$\vec{a}_P = \left.\frac{\mathrm{d}\vec{v}_P}{\mathrm{d}t}\right|_1=\left.\frac{\mathrm{d}\vec{v}_O}{\mathrm{d}t}\right|_1 + \left.\frac{\mathrm{d}\vec{\omega}}{\mathrm{d}t}\right|_1\times\overrightarrow{OP}+\vec{\omega}\times\left.\frac{\mathrm{d}(\overrightarrow{OP})}{\mathrm{d}t}\right|_1$

Siendo

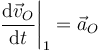
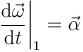
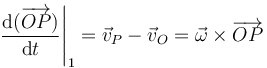
$\left.\frac{\mathrm{d}\vec{v}_O}{\mathrm{d}t}\right|_1=\vec{a}_O$ $\left.\frac{\mathrm{d}\vec{\omega}}{\mathrm{d}t}\right|_1=\vec{\alpha}$ $\left.\frac{\mathrm{d}(\overrightarrow{OP})}{\mathrm{d}t}\right|_1=\vec{v}_P-\vec{v}_O = \vec{\omega}\times\overrightarrow{OP}$

llegamos a la expresión del campo de aceleraciones

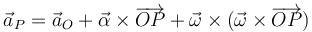
$\vec{a}_P = \vec{a}_O + \vec{\alpha}\times\overrightarrow{OP} + \vec{\omega}\times(\vec{\omega}\times\overrightarrow{OP})$

3.2 Caso de campo de velocidades conocido

Al mismo resultado se llega, como no puede ser de otra forma, si lo que conocemos es el campo de velocidades en el sistema fijo en todo instante.

Se trata de relacionar la expresión para la aceleración de P con la correspondiente a otros puntos. Tenemos que en todo instante la velocidad en P cumple

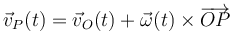
$\vec{v}_P(t)=\vec{v}_O(t)+\vec{\omega}(t)\times\overrightarrow{OP}$

de manera que la aceleración de P viene dada por

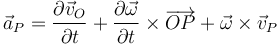
$\vec{a}_P=\frac{\partial \vec{v}_O}{\partial t}+\frac{\partial\vec{\omega}}{\partial t}\times\overrightarrow{OP}+\vec{\omega}\times\vec{v}_P$

(ahora $\overrightarrow{OP}$ es un vector constante, pues estamos tomando O y P del sistema fijo). A la derivada de la velocidad angular se la denomina aceleración angular

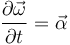
$\frac{\partial\vec{\omega}}{\partial t}=\vec{\alpha}$

Es indiferente que sea una derivada parcial o una total, ya que $\vec{\omega}$ no depende más que del tiempo.

Si sustituimos la aceleración de O nos queda

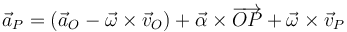
$\vec{a}_P=\left(\vec{a}_O-\vec{\omega}\times\vec{v}_O\right)+\vec{\alpha}\times\overrightarrow{OP}+\vec{\omega}\times\vec{v}_P$

Sustituimos de nuevo la expresión del campo de velocidades y llegamos a la expresión del campo de aceleraciones

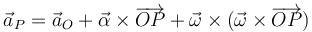
$\vec{a}_P = \vec{a}_O + \vec{\alpha}\times\overrightarrow{OP} + \vec{\omega}\times(\vec{\omega}\times\overrightarrow{OP})$

A diferencia del campo de velocidades, el campo de aceleraciones no es equiproyectivo:

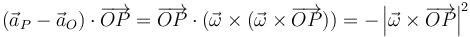
$(\vec{a}_P-\vec{a}_O)\cdot\overrightarrow{OP}=\overrightarrow{OP}\cdot(\vec{\omega}\times(\vec{\omega}\times\overrightarrow{OP})) = -\left|\vec{\omega}\times\overrightarrow{OP}\right|^2$

Solo en el caso de traslación o reposo instantáneos se cumplirá la equiproyectividad.

Dos consideraciones prácticas.

El campo de aceleraciones requiere conocer tres vectores (esto es, 9 datos, frente a los 6 del campo de velocidades):
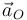- La aceleración de un punto O, $\vec{a}_O$ .
- La velocidad angular instantánea, $\vec{\omega}$ .
- La aceleración angular, 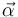$\vec{\alpha}$ , derivada temporal de la velocidad angular.
La aceleración de un punto P se puede calcular derivando la velocidad sólo si se conoce ésta como función del tiempo 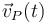$\vec{v}_P(t)$ . Conocerla en un instante no es suficiente.

El conocimiento del campo de aceleraciones es especialmente útil cuando tenemos un punto fijo O, para el cual 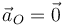$\vec{a}_O=\vec{0}$ y deseamos hallar la aceleración de otro punto en concreto, en particular, del centro de masas del sólido.

Campo de aceleraciones de un sólido

De Laplace

Contenido

1 Introducción

2 Aceleración de un punto

3 Campo de aceleraciones

3.1 Caso de movimiento de O conocido

3.2 Caso de campo de velocidades conocido

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES