Asociaciones de resortes
De Laplace
Contenido |
1 Enunciado
Determine la frecuencia de oscilación de una masa m unida a dos muelles de constantes k1 y k2 cuando
- los muelles están conectados en paralelo.
- los muelles están conectados en serie.
2 Solución
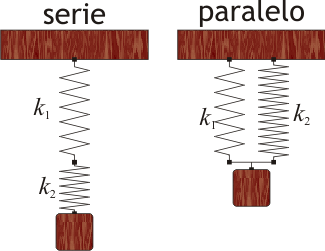
Previamente al cálculo hay que definir qué entendemos por asociación en serie o en paralelo. El concepto es análogo al de las asociaciones de elementos en un circuito. Dos resortes estarán
- en paralelo, cuando están conectados por sus dos extremos,
- en serie, cuando lo están solo por uno de ellos y en el punto de conexión no hay conectado ningún resorte adicional.
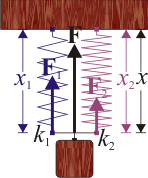
2.1 Muelles en paralelo
Por simplicidad supondremos el caso unidimensional, aunque resultados análogos se tienen en el caso general tridimensional. Igualmente, para facilitar la visualización del sistema, consideraremos que están situados verticalmente y un peso mg cuelga de ellos.
La masa está unida al techo a través de dos resortes, de constantes k1 y k2. Cuando la masa desciende una cantidad x, los dos muelles se estirarán en la misma cantidad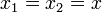
La fuerza total que los muelles ejercen sobre la masa será su resultante
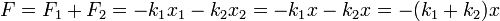
Por tanto, la asociación se comporta como un solo muelle, cuya constante es la suma de las constantes
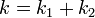
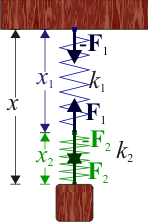
2.2 Muelles en serie
Consideremos ahora dos mueles puestos uno a continuación del otro. El muelle 1 se encuentra anclado a la pared y se estirará una cantidad x1. El muelle 2 se encuentra anclado a éste, y se estirará una cantidad
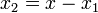

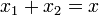
La fuerza sobre la masa m, situada en el extremo libre del muelle 2, es ejercida por este muelle
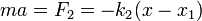
¿Cuánto vale x1? Una forma de hallarlo es considerar, temporalmente, que en el punto de unión tenemos una pequeña masa m0
Esa masa está unida a dos muelles, uno de constante k1, unido a la pared, y otro de constante k2, unido a la masa m. La 2ª ley de Newton, para esta masa intermedia se leerá
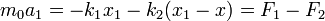
Si ahora consideramos que esa masa en realidad no está ahí, esto equivale a hacer 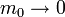 y por tanto
y por tanto
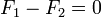

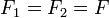
Por tanto
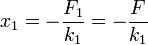
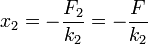
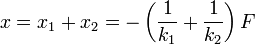
y la constante equivalente a la asociación en serie cumple
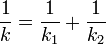

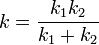
Resumiendo, de forma análoga a como ocurre con los condensadores en los circuitos:
- Si los muelles están en paralelo, la constante de la asociación es la suma de las constantes
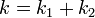
- Si los muelles están en serie, la inversa de la constante es la suma de las inversas
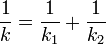
A partir de aquí ya se pueden considerar casos más complicados, como asociaciones en serie de asociaciones en paralelo y situaciones por el estilo.