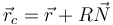Aceleración de una partícula (CMR)
De Laplace
Contenido |
1 Definición
Se define la aceleración instantánea como la derivada de la velocidad respecto al tiempo
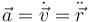
En una base fija, las componentes de la aceleración son las derivadas temporales de las componentes de la velocidad (y la segunda derivada de las de la posición)
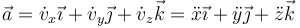
2 Componentes intrínsecas
Derivando la expresión de la velocidad como producto de la rapidez y el vector tangente
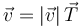
queda
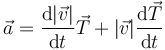
El primero de los dos sumandos es paralelo al vector tangente y a la velocidad. El segundo es ortogonal a  , por ser éste un vector de módulo constante. Por tanto, la aceleración se puede escribir como suma de una aceleración tangencial, responsable del cambio en la rapidez, y de una aceleración normal, asociada al cambio en la dirección del movimiento.
, por ser éste un vector de módulo constante. Por tanto, la aceleración se puede escribir como suma de una aceleración tangencial, responsable del cambio en la rapidez, y de una aceleración normal, asociada al cambio en la dirección del movimiento.

Estas dos componentes pueden también hallarse proyectando sobre la velocidad
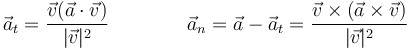
3 Triedro de Frenet
Como hemos visto, a partir de la velocidad puede definirse un unitario tangente a la trayectoria
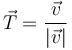
y a partir de la aceleración normal podemos definir un vector unitario normal a la trayectoria
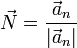
Este vector es siempre ortogonal a la trayectoria y hacia adentro de las curvas que describe.
Completamos un triedro (denominado triedro de Frenet) mediante el producto de estos dos, obteniendo el vector binormal
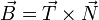
Cualquier vector puede expresarse como cominación lineal de este triedro
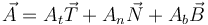
En particular
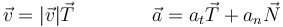
A diferencia de la base cartesiana, el triedro de Frenet es una función del tiempo, ya que se desplaza y gira con la partícula en su movimiento. Por ello, cualquier derivada respecto al tiempo deberá tener en cuenta las derivadas de estos vectores.
4 Curvatura
La curvatura de una trayectoria mide como cambia la dirección de esta. Se define a partir de la derivada del vector tangente como
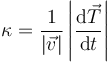
La inversa de la curvatura es el denominado radio de curvatura
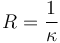
de forma que la aceleración normal puede escribirse en la forma

El centro de curvatura se define como el punto móvil