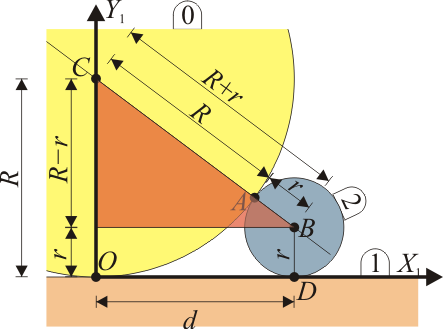
Deslizamiento entre dos rodillos

De Laplace

Revisión a fecha de 17:10 26 ago 2017; Antonio (Discusión | contribuciones)

(dif) ← Revisión anterior | Revisión actual (dif) | Revisión siguiente → (dif)

Contenido

1 Enunciado
2 Introducción
3 Velocidad del sólido 0
- 3.1 Empleando la velocidad angular
- 3.2 Sin emplear la velocidad angular
4 Velocidad del sólido 2
5 Velocidad de deslizamiento

1 Enunciado

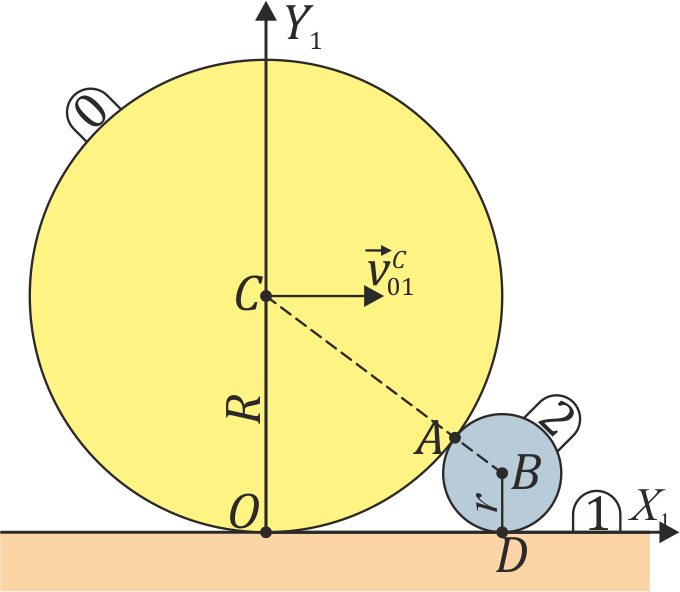
Un rodillo de radio 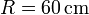$R=60\,\mathrm{cm}$ (sólido “0”) rueda sin deslizar sobre un suelo horizontal “1” de forma que su centro $C$ avanza con una celeridad constante 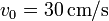$v_0=30\,\mathrm{cm}/\mathrm{s}$ respecto al suelo. En su marcha, este rodillo empuja a un segundo rodillo de radio 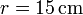$r=15\,\mathrm{cm}$ (sólido “2”), que se ve obligado a rodar sin deslizar sobre el mismo suelo, manteniéndose tangente al primer rodillo (ver figura).

Halle la velocidad relativa de deslizamiento en el punto A de contacto entre los dos sólidos. ¿Cuál es la rapidez de este deslizamiento?

2 Introducción

El deslizamiento entre los dos rodillos se debe a que ambos ruedan sobre el suelo, con lo que necesariamente la velocidad del punto A de un rodillo y la del punto A correspondiente del segundo será diferente, de forma que uno de los rodillos resbala sobre el otro.

La velocidad de deslizamiento será la diferencia de las velocidades respectivas

$\vec{v}^A_d = \vec{v}^A_{21}-\vec{v}^A_{01}$

donde con el subíndice 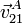$\vec{v}^A_{21}$ se indica la velocidad de un punto A del rodillo pequeño “2” respecto a “1” (el suelo). Del mismo modo con 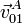$\vec{v}^A_{01}$ se indica la velocidad del mismo punto como parte del rodillo grande “0” respecto al suelo “1”.

Calcularemos por separado estas dos velocidades y posteriormente hallaremos su diferencia. Si los cálculos son correctos debe resultarnos una velocidad tangente a la superficie de contacto.

3 Velocidad del sólido 0

Del rodillo grande conocemos la velocidad de su centro, que medida en cm/s vale

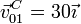
$\vec{v}^C_{01}=30\vec{\imath}$

También sabemos que rueda sin deslizar sobre el suelo, por lo que

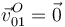
$\vec{v}^O_{01} = \vec{0}$

También sabemos que el movimiento es plano, lo que implica que la velocidad de todos los puntos del sólido está contenida en el plano XY y que su velocidad angular va en la dirección del eje Z.

Con estos dos datos debemos determinar la velocidad del punto A. Existen varias formas de hacerlo.

3.1 Empleando la velocidad angular

Una de ellas consiste en observar que el punto O es el centro instantáneo de rotación del rodillo respecto al suelo y por tanto

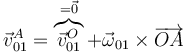
$\vec{v}^A_{01} = \overbrace{\vec{v}^O_{01}}^{=\vec{0}}+\vec{\omega}_{01}\times\overrightarrow{OA}$

Todavía no conocemos la velocidad con la rueda el rodillo, pero la podemos obtener de que conocemos la velocidad del punto C. La misma fórmula anterior la podemos aplicar al cálculo de la velocidad de C

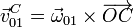
$\vec{v}^C_{01}=\vec{\omega}_{01}\times\overrightarrow{OC}$

y conocemos tanto la velocidad como la posición de C. Sustituyendo

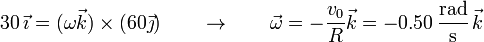
$30\,\vec{\imath} = (\omega \vec{k})\times(60\vec{\jmath}) \qquad\rightarrow\qquad \vec{\omega} = -\frac{v_0}{R}\vec{k} = -0.50\,\frac{\mathrm{rad}}{\mathrm{s}}\,\vec{k}$

Para aplicar ahora esta velocidad angular al cálculo de la velocidad de A, debemos determinar previamente la posición de A, que aun no conocemos.

Esto lo hacemos mediante un razonamiento geométrico basado en la semejanza de triángulos

Tenemos un triángulo rectángulo cuya hipotenusa mide $(R + r)$ , uno de los catetos mide $(R - r)$ y el otro mide $d$ la distancia entre los puntos de contacto con el suelo. Por aplicación del teorema de Pitágoras

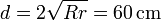
$d^2+(R-r)^2 = (R+r)^2\,$ $\Rightarrow$ $d=2\sqrt{Rr}=60\,\mathrm{cm}$

Esto nos da el vector de posición relativo entre centros (en cm)

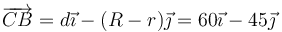
$\overrightarrow{CB}= d\vec{\imath}-(R-r)\vec{\jmath} = 60\vec{\imath}-45\vec{\jmath}$

El vector que va de C a A es proporcional al que une los dos centros

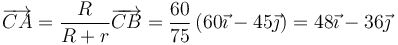
$\overrightarrow{CA}=\frac{R}{R+r}\overrightarrow{CB}= \frac{60}{75}\left(60\vec{\imath}-45\vec{\jmath}\right) = 48\vec{\imath}-36\vec{\jmath}$

y finalmente obtenemos la posición del punto A respecto al punto de contacto O

$\overrightarrow{OA}=\overrightarrow{OC}+\overrightarrow{BC} = 60\,\vec{\jmath}+(48\vec{\imath}-36\vec{\jmath}) = 48\vec{\imath}+24\vec{\jmath}$

Ahora ya sí podemos sustituir en la expresión para la velocidad de A, en cm/s

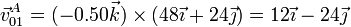
$\vec{v}^A_{01} = (-0.50\vec{k})\times(48\vec{\imath}+24\vec{\jmath}) = 12\vec{\imath}-24\vec{\jmath}$

3.2 Sin emplear la velocidad angular

Alternativamente, puede hallarse la velocidad de A sin calcular previamente la velocidad angular. Para ello, usamos la condición cinemática de rigidez. La velocidad relativa de A respecto de cualquier punto del sólido debe ser ortogonal al vector de posición relativa. Aplicando esto al punto O queda

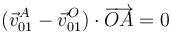
$(\vec{v}^A_{01}-\vec{v}^O_{01})\cdot\overrightarrow{OA}=0$

Sustituyendo

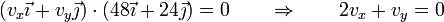
$(v_x\vec{\imath}+v_y\vec{\jmath})\cdot(48\vec{\imath}+24\vec{\jmath})=0\qquad\Rightarrow\qquad 2v_x+v_y = 0$

Aplicándolo a A y a C

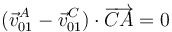
$(\vec{v}^A_{01}-\vec{v}^C_{01})\cdot\overrightarrow{CA}=0$

Sustituyendo

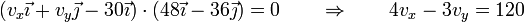
$(v_x\vec{\imath}+v_y\vec{\jmath}-30\vec{\imath})\cdot(48\vec{\imath}-36\vec{\jmath})=0\qquad\Rightarrow\qquad 4v_x-3v_y = 120$

Resolviendo el sistema de dos ecuaciones con dos incógnitas

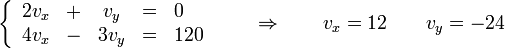
$\left\{\begin{array}{rcccl}2v_x&+&v_y & = & 0 \\ 4v_x & - & 3v_y & = & 120\end{array}\right. \qquad\Rightarrow\qquad v_x=12\qquad v_y=-24$

que, en forma vectorial nos da el resultado que ya conocemos para la velocidad de A en cm/s

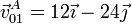
$\vec{v}^A_{01}= 12\vec{\imath}-24\vec{\jmath}$

4 Velocidad del sólido 2

Para el cálculo de la velocidad de A del rodillo 2 respecto al suelo, es cálculo es casi idéntico con la única salvedad de que ahora las posiciones deben referirse al punto de contacto D con el suelo.

La velocidad del centro B del rodillo es exactamente la misma que la de C pues los dos rodillos avanzan a la par. La velocidad angular del rodillo es entonces

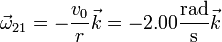
$\vec{\omega}_{21} = -\frac{v_0}{r}\vec{k}=-2.00\frac{\mathrm{rad}}{\mathrm{s}}\vec{k}$

y la velocidad del punto A en este sólido vale

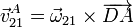
$\vec{v}^A_{21}=\vec{\omega}_{21}\times\overrightarrow{DA}$

siendo la posición relativa al punto D, en cm

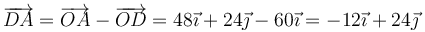
$\overrightarrow{DA} = \overrightarrow{OA}-\overrightarrow{OD}=48\vec{\imath}+24\vec{\jmath}-60\vec{\imath}= -12\vec{\imath}+24\vec{\jmath}$

con lo que la velocidad buscada vale, en cm/s,

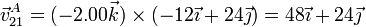
$\vec{v}^A_{21}=(-2.00\vec{k})\times(-12\vec{\imath}+24\vec{\jmath}) = 48\vec{\imath}+24\vec{\jmath}$

Esta velocidad puede también calcularse, como en el caso anterior, aplicando la condición de rigidez y resolviendo el sistema de ecuaciones resultante.

5 Velocidad de deslizamiento

Una vez que tenemos las dos velocidades respecto al suelo, hallamos la de deslizamiento como la diferencia entre ambas. El resultado es, en cm/s,

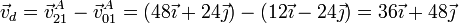
$\vec{v}_d = \vec{v}^A_{21}-\vec{v}^A_{01} = (48\vec{\imath}+24\vec{\jmath})-(12\vec{\imath}-24\vec{\jmath}) = 36\vec{\imath}+48\vec{\jmath}$

siendo la rapidez con que desliza un rodillo sobre otro

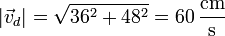
$|\vec{v}_d|=\sqrt{36^2+48^2} = 60\,\frac{\mathrm{cm}}{\mathrm{s}}$

Dijimos al principio que, como test de que el resultado no es incorrecto, podemos comprobar si la velocidad de deslizamiento es tangente a los rodillos.

Para que sea así, esta velocidad debe ser perpendicular al vector que une los dos centros

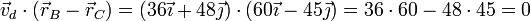
$\vec{v}_d\cdot(\vec{r}_B-\vec{r}_C) = (36\vec{\imath}+48\vec{\jmath})\cdot(60\vec{\imath}-45\vec{\jmath}) = 36\cdot 60-48\cdot 45 = 0$

Luego, efectivamente es tangente a la superficie de contacto.

Deslizamiento entre dos rodillos

De Laplace

Contenido

1 Enunciado

2 Introducción

3 Velocidad del sólido 0

3.1 Empleando la velocidad angular

3.2 Sin emplear la velocidad angular

4 Velocidad del sólido 2

5 Velocidad de deslizamiento

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES