Entrar Página Discusión Historial Go to the site toolbox

Tres superficies conductoras concéntricas (GIE)

De Laplace

Contenido

1 Enunciado

Se tiene un sistema formado por tres superficies conductoras esféricas concéntricas, de radios 2b, 3b y 6b. Inicialmente la esfera interior almacena una carga − Q0, la intermedia está aislada y descargada y la exterior almacena una carga + Q0.

  1. Calcule el potencial al que se encuentra cada esfera.
  2. Halle el campo eléctrico en los puntos del eje OZ siguientes: z = 0, z = 5b / 2, z = 4b y z = 8b, siendo el origen de coordenadas el centro de las esferas.
  3. Halle la energía almacenada en el sistema

En un momento dado se cierra el interruptor que conecta la esfera intermedia a tierra. Una vez que se alcanza de nuevo el equilibrio electrostático:

  1. ¿Cuáles son las nuevas cargas y potenciales de los tres conductores?
  2. ¿Cuánto vale ahora el campo eléctrico en los puntos del apartado 2?
  3. ¿Cuánto vale la energía almacenada en el sistema?
  4. ¿Cuánta energía se ha perdido en el proceso?

2 Antes de la conexión

2.1 Potenciales

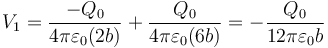
V_1=\frac{-Q_0}{4\pi\varepsilon_0(2b)}+\frac{Q_0}{4\pi\varepsilon_0(6b)}=-\frac{Q_0}{12\pi\varepsilon_0b}

 

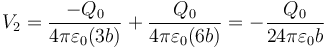
V_2=\frac{-Q_0}{4\pi\varepsilon_0(3b)}+\frac{Q_0}{4\pi\varepsilon_0(6b)}=-\frac{Q_0}{24\pi\varepsilon_0b}

 

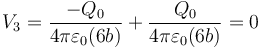
V_3=\frac{-Q_0}{4\pi\varepsilon_0(6b)}+\frac{Q_0}{4\pi\varepsilon_0(6b)}=0

2.2 Campo

\vec{E}(z=0)=\vec{0}

 

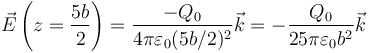
\vec{E}\left(z=\frac{5b}{2}\right)=\frac{-Q_0}{4\pi\varepsilon_0(5b/2)^2}\vec{k}=-\frac{Q_0}{25\pi\varepsilon_0b^2}\vec{k}

 

\vec{E}\left(z=4b\right)=\frac{-Q_0}{4\pi\varepsilon_0(4b)^2}\vec{k}=-\frac{Q_0}{64\pi\varepsilon_0b^2}\vec{k}

 

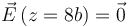
\vec{E}\left(z=8b\right)=\vec{0}

2.3 Energía

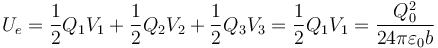
U_e=\frac{1}{2}Q_1V_1+\frac{1}{2}Q_2V_2+\frac{1}{2}Q_3V_3=\frac{1}{2}Q_1V_1=\frac{Q_0^2}{24\pi\varepsilon_0b}

3 Después de la conexión

3.1 Cargas y potenciales

3.1.1 Cargas

Q^\prime_1=-Q_0\qquad\qquad Q^\prime_3=+Q_0

 

0=V^\prime_2=-\frac{Q_0}{24\pi\varepsilon_0b}+\frac{Q^\prime_2}{4\pi\varepsilon_0(3b)}\qquad\Rightarrow\qquad Q^\prime_2=\frac{Q_0}{2}

3.1.2 Potenciales

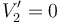
V^\prime_2=0\,

 

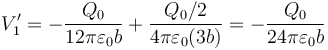
V^\prime_1=-\frac{Q_0}{12\pi\varepsilon_0b}+\frac{Q_0/2}{4\pi\varepsilon_0(3b)}=-\frac{Q_0}{24\pi\varepsilon_0b}

 

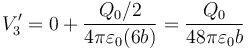
V^\prime_3=0+\frac{Q_0/2}{4\pi\varepsilon_0(6b)}=\frac{Q_0}{48\pi\varepsilon_0b}

3.2 Campo

\vec{E}^\prime(z=0)=\vec{0}

 

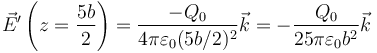
\vec{E}^\prime\left(z=\frac{5b}{2}\right)=\frac{-Q_0}{4\pi\varepsilon_0(5b/2)^2}\vec{k}=-\frac{Q_0}{25\pi\varepsilon_0b^2}\vec{k}

 

\vec{E}^\prime\left(z=4b\right)=\frac{-Q_0}{4\pi\varepsilon_0(4b)^2}\vec{k}+\frac{Q_0/2}{4\pi\varepsilon_0(4b)^2}\vec{k}=-\frac{Q_0}{128\pi\varepsilon_0b^2}\vec{k}

 

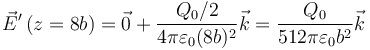
\vec{E}^\prime\left(z=8b\right)=\vec{0}+\frac{Q_0/2}{4\pi\varepsilon_0(8b)^2}\vec{k}=\frac{Q_0}{512\pi\varepsilon_0b^2}\vec{k}

3.3 Energía

3.3.1 Energía final

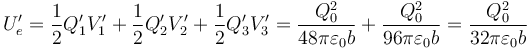
U^\prime_e=\frac{1}{2}Q^\prime_1V^\prime_1+\frac{1}{2}Q^\prime_2V^\prime_2+\frac{1}{2}Q^\prime_3V^\prime_3=\frac{Q_0^2}{48\pi\varepsilon_0b}+\frac{Q_0^2}{96\pi\varepsilon_0b}=\frac{Q_0^2}{32\pi\varepsilon_0b}

3.3.2 Energía disipada

\Delta U_e=\frac{Q_0^2}{32\pi\varepsilon_0b}-\frac{Q_0^2}{24\pi\varepsilon_0b}=-\frac{Q_0^2}{96\pi\varepsilon_0b}
Obtenido de "http://tesla.us.es/wiki/index.php/Tres_superficies_conductoras_conc%C3%A9ntricas_(GIE)"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Aviso legal - Acerca de Laplace