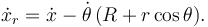Engranaje sobre cremallera (MR G.I.C.)
De Laplace
Contenido |
1 Enunciado
La figura muestra un sistema mecánico formado por un engranaje que rueda sobre una cremallera y está conectado a un deslizador con una ranura que desliza respecto al pasador en B. El deslizador está acoplado a un muelle, de constante elástica k, que se encuentra relajado cuando x = 2R. En ese instante se tiene θ = 0. Las masas del engranaje, el deslizador y la cremallera son mA, mS y mr, respectivamente. El contacto entre el pasador y la ranura es liso. El mecanismo es accionado por una fuerza aplicada sobe la cremallera como se indica en la figura.
- Encuentra el número de grados de libertad y elige un conjunto de coordenadas generalizadas para describir el movimiento.
- Encuentra las ecuaciones diferenciales del movimiento.
2 Solución
2.1 Grados de libertad
En el dibujo se identifican tres coordenadas: xr, x y θ. Sin embargo el problema tiene sólo dos grados de libertad. Podemos verlo a partir del número de ligaduras que se imponen entre los sólidos. Tenemos tres sólidos haciendo un movimiento plano, luego a priori hay 9 grados de libertad, 3 por cada sólido. Las ligaduras son
- {01}: traslación: 2 ligaduras.
- {31}: traslación: 2 ligaduras.
- {20}: rodadura sin deslizamiento en C: 2 ligaduras.
- {32}:
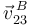 debe ser paralela a Y1: 1 ligadura.
debe ser paralela a Y1: 1 ligadura.
Esto hace en total 7 ligaduras. Por tanto el número de grados de libertad es
r = 9 − 7 = 2.
2.2 Relación entre las coordenadas
Vamos a obtener las reducciones cinemáticas de los movimientos relativos para encontrar la relación entre las ligaduras.
2.2.1 Movimiento {01}
Es la traslación de la cremallera respecto al suelo

Al ser una traslación no hay que especificar el punto en la velocidad.
2.2.2 Movimiento {31}
También es una traslación respecto al suelo

2.2.3 Movimiento {20}
Es una rodadura sin deslizamiento en C

2.2.4 Movimiento {23}
Este es el movimiento que nos va a dar la relación que buscamos. La ligadura es
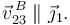
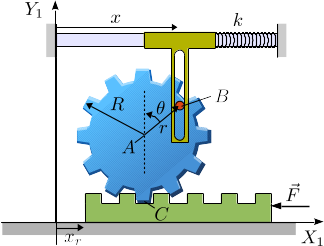
Usando composición de movimientos tenemos

Para cada movimiento tenemos
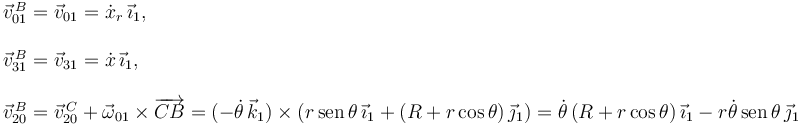
Entonces
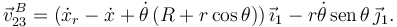
La componente en 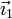 tiene que ser cero. Por tanto
tiene que ser cero. Por tanto