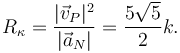Partícula moviéndose sobre una parábola, Noviembre 2016 (G.I.C.)
De Laplace
Contenido |
1 Enunciado
2 Partícula moviéndose sobre una parábola
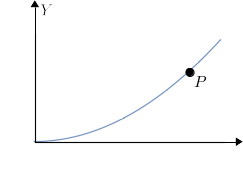
Una partícula recorre una parábola de ecuación y = x2 / k, siendo k una constante. La partícula se mueve de modo que la velocidad sobre el eje OX es constante e igual a v0. En el instante inicial la partícula se encontraba en el origen de coordenadas.
- Determina las unidades base de k en el S.I.
- Calcula el vector de posición de la partícula.
- Determina la aceleración de la partícula.
- Calcula el vector aceleración normal en el instante de tiempo t0 = k / v0.
- En ese mismo instante, calcula el valor del radio de curvatura.
3 Solución
3.1 Unidades de k
Consideremos la expresión
y = x2 / k.
Tanto y como x son coordenadas espaciales, por tanto su unidad base en el S.I. es el metro. Para que los dos términos sean dimensionalmente coherentes debe ocurrir que
[k] = m.
3.2 Vector de posición
Como el movimiento transcurre en el plano OXY, en todo instante tenemos
z = 0
Entonces el vector de posición de la partícula puede escribirse
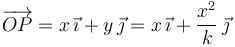
Hemos usado la expresión de la curva dada en el enunciado. Como el movimiento sobre el eje OX es uniforme, con velocidad constante v0, y en el instante inicial se tiene x(0) = 0, tenemos
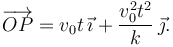
3.3 Vector aceleración
Derivamos una vez respecto del tiempo para obtener la velocidad
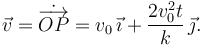
Derivando otra vez respecto del tiempo tenemos la aceleración
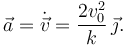
3.4 Velocidad normal y radio de curvatura en t0 = k / v0
En el instante t0 = k / v0 tenemos
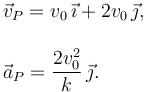
El módulo de la velocidad en ese instante es
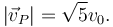
El vector tangente en ese instante es
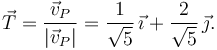
La aceleración tangencial es
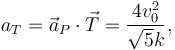
el vector aceleración tangencial es
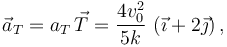
y el vector aceleración normal es
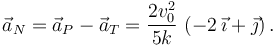
El radio de curvatura en ese instante es