Entrar Página Discusión Historial Go to the site toolbox

Movimientos rígidos (CMR)

De Laplace

Contenido

1 El modelo del sólido rígido

1.1 Condición geométrica de rigidez

1.2 Condición cinemática de rigidez

2 Sólidos y sistemas de referencia

3 Movimientos rígidos finitos. Matriz de rotación

Un movimiento rígido de un sólido es aquel que preserva las distancias entre cada par de puntos, de forma que si una partícula se encuentra inicialmente en el punto A0 y posteriormente en el punto A y lo mismo co partículas B, C,… se cumple en todo instante

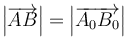
\left|\overrightarrow{AB}\right| = \left|\overrightarrow{A_0B_0}\right|

y al cumplirse para todos los puntos esto implica igualmente la conservación de los ángulos

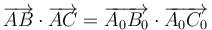
\overrightarrow{AB}\cdot\overrightarrow{AC}=\overrightarrow{A_0B_0}\cdot\overrightarrow{A_0C_0}

Existen diferentes transformaciones que mantienen las distancias y los ángulos:

Traslaciones
Todos los puntos experimentan el mismo desplazamiento, preservándose la orientación del sólido
\overrightarrow{A_0A}=\overrightarrow{B_0B}\qquad\qquad \overrightarrow{A_0B_0} = \overrightarrow{AB}
Rotaciones
Existe al menos un punto cuya posición no se ve modificada. El resto e puntos experimenta un desplzamiento perpendicular a dicho eje.
Simetría
Se invierten las posiciones respectoa un plano de simetría. Un movimiento real de un sólido nunca puede consistir en una simetría (debería “volverse del revés”) por lo que no las consideremos en este artículo.

Un teorema crucial en la cinemática del sólido es que todo movimiento real puede descomponerse en una traslación y una rotación.

Para ello consideramos un partícula del sólido que inicialmente se hallaba en A0 y posteriormente en A. Este punto experimenta un desplazamiento

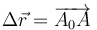
\Delta\vec{r}=\overrightarrow{A_0A}

Supongamos que sometemos a todo el sólido a una traslación 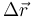\Delta\vec{r}. para pasar de este estado intermedio al estado final debemos efectuar otro movimiento rígido en el que A es un punto fijo (porque ya se ha movido todo lo que se tenía que mover). Este segundo movimiento será entonces una rotacón alrededor de A.

El punto A no tiene nada de especial. Podemos aplicar el mismo razonamiento a cualquier otro punto de referencia y el resultado es el mismo, es más, aunque el desplzamiento variará en cada caso, la rotación que debemos efectuar es independiente del punto de referencia que hayamos tomado.

Para ello consideramos el movimiento respecto a un punto dado A del sólido. Este punto experimenta un cirto desplazamiento. El resto de los puntos eperimenta el mismo desplzamiento que A más un movimiento rígido alrededor de A, que constituye una rotación.

3.1 Expresión de las traslaciones

En términos de las componentes cartesianas, una traslación se calcula sumando las componentes del desplazamiento

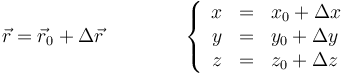
\vec{r}=\vec{r}_0+\Delta \vec{r}\qquad\qquad \left\{ \begin{array}{rcl} x & = & x_0+ \Delta x \\ y & = & y_0+ \Delta y \\ z & = & z_0+ \Delta z \end{array}\right.

3.2 Expresión de las rotaciones

Supongamos que en una rotación el punto fijo es O, que tomaremos como origen de coordenadas. En una rotación, cualquier punto pasará de la posición

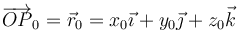
\overrightarrow{OP}_0=\vec{r}_0=x_0\vec{\imath}+y_0\vec{\jmath}+z_0\vec{k}

a la posición

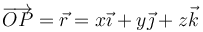
\overrightarrow{OP}=\vec{r}=x\vec{\imath}+y\vec{\jmath}+z\vec{k}

Deseamos establecer la relación entre estos dos vectores.

Para ello, emplearemos dos sistemas de referencia. El sistema “1” es el que consideramos fijo y respecto al cual se mueve el sólido. Los dos vectores que avabamos de escribir estarían expresados en la base 1. El otro (“0”) es uno móvil que gira con el sólido en todo momento.

En ese caso, al estar ligado al sólido, la posición de los puntos de éste son constantes en todo momento. Es decir, la posición de P

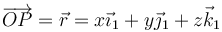
\overrightarrow{OP}=\vec{r}=x\vec{\imath}_1+y\vec{\jmath}_1+z\vec{k}_1

se expresará en la base 0

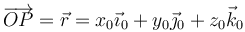
\overrightarrow{OP}=\vec{r}=x_0\vec{\imath}_0+y_0\vec{\jmath}_0+z_0\vec{k}_0

Nótese que en ambos casos se trata del mismo vector, expresado en dos bases distintas.

Para hallar las componentes en la base 1 proyectamos sobre cada vector de esta base

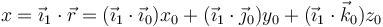
x = \vec{\imath}_1\cdot\vec{r} = (\vec{\imath}_1\cdot\vec{\imath}_0)x_0+(\vec{\imath}_1\cdot\vec{\jmath}_0)y_0 + (\vec{\imath}_1\cdot\vec{k}_0)z_0

y análogamente para las otras dos componentes. Podemos escribir este resultado en forma matricial

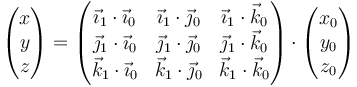
\begin{pmatrix}x \\ y \\ z\end{pmatrix}=\begin{pmatrix} \vec{\imath}_1\cdot\vec{\imath}_0 & \vec{\imath}_1\cdot\vec{\jmath}_0 & \vec{\imath}_1\cdot\vec{k}_0 \\ \vec{\jmath}_1\cdot\vec{\imath}_0 & \vec{\jmath}_1\cdot\vec{\jmath}_0 & \vec{\jmath}_1\cdot\vec{k}_0 \\ \vec{k}_1\cdot\vec{\imath}_0 & \vec{k}_1\cdot\vec{\jmath}_0 & \vec{k}_1\cdot\vec{k}_0 \end{pmatrix}\cdot \begin{pmatrix}x_0 \\ y_0 \\ z_0\end{pmatrix}

que podemos abreviar como

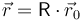
\vec{r}=\mathsf{R}\cdot\vec{r}_0

donde 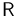\mathsf{R} es la matriz de rotación que relaciona las componentes iniciales del vector de posición (o las que tiene en una base ligada al sólido) con las que tiene en un instante posterior. Esta matriz será función del tiempo.

Vemos que los elementos de la matriz de rotación son los productos escalares entre los vectores de la base fija en el sólido y la fija en el laboratorio. Por ser unitarios todos los vectores estos elementos son los cosenos directores

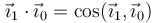
\vec{\imath}_1\cdot\vec{\imath}_0 = \cos(\vec{\imath}_1,\vec{\imath}_0)

Asmismo, cada fila corresponde a las componentes de un vector de la base fija (1) expresado en la base ligada al sólido (0), y cada columna un vector de la base ligada al sólido expresado en la base fija. Simbólicamente

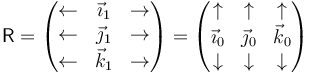
\mathsf{R}=\begin{pmatrix}\leftarrow & \vec{\imath}_1 & \rightarrow \\ \leftarrow & \vec{\jmath}_1 & \rightarrow \\ \leftarrow & \vec{k}_1 & \rightarrow \end{pmatrix} = \begin{pmatrix} \uparrow & \uparrow & \uparrow \\ \vec{\imath}_0 & \vec{\jmath}_0 & \vec{k}_0 \\ \downarrow & \downarrow & \downarrow\end{pmatrix}

3.2.1 Propiedades de la matriz de rotación

Tiene tres grados de libertad
De acuerdo con la expresión anterior, parece que para expresar una rotación hay que proporcionar 9 parámetros, esto es, que tiene 9 grados de libertad. No es así, ya que tenemos seis vínculos entre las componentes. Por ser ortonormal cada base
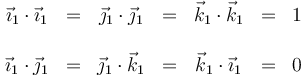
\begin{array}{ccccccc} \vec{\imath}_1\cdot\vec{\imath}_1 & = & \vec{\jmath}_1\cdot\vec{\jmath}_1 & = & \vec{k}_1\cdot\vec{k}_1& = & 1\\ &&&&&& \\ \vec{\imath}_1\cdot\vec{\jmath}_1 & = & \vec{\jmath}_1\cdot\vec{k}_1 & = & \vec{k}_1\cdot\vec{\imath}_1& = & 0\end{array}
Estos seis vínculos reducen el número de grados de libertad a 3, que pueden ser tres ángulos de orientación, como los ángulos de Euler.
Es ortogonal
Una matriz es ortogonal cuando su traspuesta coincide con su inversa. Si una rotación dada lleva de la base 1 a la base 0, la rotación inversa será la que devuelve la base 0 a la base 1. Por la construcción de la matriz, el intercambiar 1 por 0 equivale a intercambiar filas por columnas, esto es, hallar la traspuesta. Por tanto
\mathsf{R}^{-1}=\mathsf{R}^T\,\qquad\Rightarrow\qquad \mathsf{R}^T\mathsf{R}=\mathsf{R}\mathsf{R}^T=\mathsf{I}
Esta propiedad equivale a lo que hemos mencionado de que las dos bases 0 y 1 son bases ortonormales.
Es unitaria
Una matriz es unitaria si su determinante vale la unidad. Es consecuencia inmediata de lo anterior
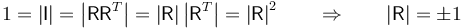
1=\left|\mathsf{I}\right|=\left|\mathsf{R}\mathsf{R}^T\right|=\left|\mathsf{R}\right|\left|\mathsf{R}^T\right|=\left|\mathsf{R}\right|^2\qquad\Rightarrow\qquad \left|\mathsf{R}\right|=\pm 1
La raíz negativa la descartamos, ya que corresponde a las simetrías, que hemos considerado como imposibles en el movimiento de un sólido real.

3.2.2 Teorema de Euler. Eje de rotación

Hemos definido como un movimiento rígido que deja un punto fijo. Euler demostró que esto implica que no hay un solo punto fijo, sino toda una recta que pasa por O. Esta recta es el llamado eje de rotación.

La demostración se basa en que debe haber un vector no afectado por la rotación, esto es,

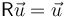
\mathsf{R}\vec{u}=\vec{u}

Si este vector \vec{u} existe, cualquier múltiplo de él tampoco se verá afectado, con lo que obtenemos toda una recta que pasa por O.

En términos algebraicos esto equivale a decir que existe un autovalor unidad, siendo \vec{u} el autovector correspondiente. La condición para que ello ocurra es que

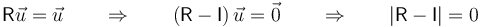
\mathsf{R}\vec{u}=\vec{u}\qquad\Rightarrow\qquad \left(\mathsf{R}-\mathsf{I}\right)\vec{u}=\vec{0}´\qquad\Rightarrow\qquad \left|\mathsf{R}-\mathsf{I}\right|=0

Veamos que es cierto:

No se pudo entender (Falta el ejecutable de <strong>texvc</strong>. Por favor, lea <em>math/README</em> para configurarlo.): \left|\mathsf{R}-\mathsf{I}\right|=\left|(\mathsf{R}-\mathsf{I})^T\right|=\left|\mathsf{R}^T-\mathsf{I}\right|=\left|\mathsf{R}^T(\mathsf{I}-\mathsf{R}\right)\right|=\left|\mathsf{R}^T\right|\left|\mathsf{I}-\mathsf{R}\right|=-\left|\mathsf{R}-\mathsf{I}\right|

y por tanto

\left|\mathsf{R}-\mathsf{I}\right|=-\left|\mathsf{R}-\mathsf{I}\right|\qquad\Rightarrow\qquad \left|\mathsf{R}-\mathsf{I}\right|=0

3.3 Propiedades de la matrix de rotación

Tiene tres grados de libertad
De acuerdo con la expresión anterior, parece que para expresar una rotación hay que proporcionar 9 parámetros, esto es, que tiene 9 grados de libertad. No es así, ya que tenemos seis vínculos entre las componentes. Por ser ortonormal cada base
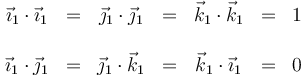
\begin{array}{ccccccc} \vec{\imath}_1\cdot\vec{\imath}_1 & = & \vec{\jmath}_1\cdot\vec{\jmath}_1 & = & \vec{k}_1\cdot\vec{k}_1& = & 1\\ &&&&&& \\ \vec{\imath}_1\cdot\vec{\jmath}_1 & = & \vec{\jmath}_1\cdot\vec{k}_1 & = & \vec{k}_1\cdot\vec{\imath}_1& = & 0\end{array}
Estos seis vínculos reducen el número de grados de libertad a 3, que pueden ser tres ángulos de orientación, como los ángulos de Euler.

4 Campo de velocidades

5 Campo de aceleraciones

6 Movimiento plano de un sólido

7 Sólido con un eje fijo

Obtenido de "http://tesla.us.es/wiki/index.php/Movimientos_r%C3%ADgidos_(CMR)"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Aviso legal - Acerca de Laplace