Movimientos rígidos (CMR)
De Laplace
Contenido |
1 El modelo del sólido rígido
1.1 Condición geométrica de rigidez
1.2 Condición cinemática de rigidez
2 Sólidos y sistemas de referencia
3 Movimientos rígidos finitos. Matriz de rotación
Un movimiento rígido de un sólido es aquel que preserva las distancias entre cada par de puntos, de forma que si una partícula se encuentra inicialmente en el punto A0 y posteriormente en el punto A y lo mismo co partículas B, C,… se cumple en todo instante
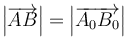
y al cumplirse para todos los puntos esto implica igualmente la conservación de los ángulos
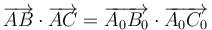
Existen diferentes transformaciones que mantienen las distancias y los ángulos:
- Traslaciones
- Todos los puntos experimentan el mismo desplazamiento, preservándose la orientación del sólido

- Rotaciones
- Existe al menos un punto cuya posición no se ve modificada. El resto e puntos experimenta un desplzamiento perpendicular a dicho eje.
- Simetría
- Se invierten las posiciones respectoa un plano de simetría. Un movimiento real de un sólido nunca puede consistir en una simetría (debería “volverse del revés”) por lo que no las consideremos en este artículo.
Un teorema crucial en la cinemática del sólido es que todo movimiento real puede descomponerse en una traslación y una rotación.
Para ello consideramos un partícula del sólido que inicialmente se hallaba en A0 y posteriormente en A. Este punto experimenta un desplazamiento
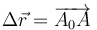
Supongamos que sometemos a todo el sólido a una traslación 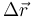 . para pasar de este estado intermedio al estado final debemos efectuar otro movimiento rígido en el que A es un punto fijo (porque ya se ha movido todo lo que se tenía que mover). Este segundo movimiento será entonces una rotacón alrededor de A.
. para pasar de este estado intermedio al estado final debemos efectuar otro movimiento rígido en el que A es un punto fijo (porque ya se ha movido todo lo que se tenía que mover). Este segundo movimiento será entonces una rotacón alrededor de A.
El punto A no tiene nada de especial. Podemos aplicar el mismo razonamiento a cualquier otro punto de referencia y el resultado es el mismo, es más, aunque el desplzamiento variará en cada caso, la rotación que debemos efectuar es independiente del punto de referencia que hayamos tomado.
Para ello consideramos el movimiento respecto a un punto dado A del sólido. Este punto experimenta un cirto desplazamiento. El resto de los puntos eperimenta el mismo desplzamiento que A más un movimiento rígido alrededor de A, que constituye una rotación.
3.1 Expresión de las traslaciones
En términos de las componentes cartesianas, una traslación se calcula sumando las componentes del desplazamiento
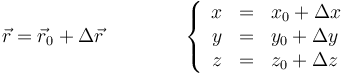
3.2 Expresión de las rotaciones
Expetenda tincidunt in sed, ex partem placerat sea, porro commodo ex eam. His putant aeterno interesset at. Usu ea mundi tincidunt, omnium virtute aliquando ius ex. Ea aperiri sententiae duo. Usu nullam dolorum quaestio ei, sit vidit facilisis ea. Per ne impedit iracundia neglegentur. Consetetur neglegentur eum ut, vis animal legimus inimicus id.
His audiam deserunt in, eum ubique voluptatibus te. In reque dicta usu. Ne rebum dissentiet eam, vim omnis deseruisse id. Ullum deleniti vituperata at quo, insolens complectitur te eos, ea pri dico munere propriae. Vel ferri facilis ut, qui paulo ridens praesent ad. Possim alterum qui cu. Accusamus consulatu ius te, cu decore soleat appareat usu.




