Cantidad de movimiento (CMR)

De Laplace

Revisión a fecha de 15:05 15 oct 2016; Antonio (Discusión | contribuciones)

(dif) ← Revisión anterior | Revisión actual (dif) | Revisión siguiente → (dif)

Contenido

1 Definición
2 Teorema de la cantidad de movimiento
3 Impulso
4 Ejemplo: colisión con una pared
- 4.1 Pared estacionaria
- 4.2 Pared en movimiento
5 Teorema de conservación de la cantidad de movimiento
6 Conservación parcial de la cantidad de movimiento

1 Definición

Se define la cantidad de movimiento de una partícula como el producto de su masa por su velocidad

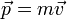
$\vec{p}=m\vec{v}\,$

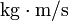Sus dimensiones son $M L T - 1$ y sus unidades en el SI son $\mathrm{N}\cdot\mathrm{s}$ (o $\mathrm{kg}\cdot\mathrm{m}/\mathrm{s}$ )

2 Teorema de la cantidad de movimiento

A partir de la definición es inmediato que

$\frac{\mathrm{d}\vec{p}}{\mathrm{d}t}=m\frac{\mathrm{d}\vec{v}}{\mathrm{d}t}=m\vec{a} = \vec{F}$

esto es, la derivada respecto al tiempo de la cantidad de movimiento es igual a la resultante de las fuerzas aplicadas sobre la partícula.

En el caso de una sola partícula, el teorema de la cantidad de movimiento no es más que la segunda ley de Newton. Este teorema cobra interés cuando se generaliza a sistemas de partículas.

3 Impulso

En ocasiones, no nos interesa tanto saber cómo cambia la cantidad de movimiento en un intervalo de tiempo infinitesimal, sino saber cuánto varía durante un cierto periodo. Supongamos una partícula que viaja libremente y por tanto con cantidad de movimiento constante 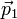$\vec{p}_1$ . Entonces es sometida a una fuerza 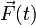$\vec{F}(t)$ durante un intervalo entre $t 1$ y $t 2$ (por ejemplo, durante una colisión), a partir del cual vuelve a moverse libremente, con cantidad de movimiento constante 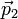$\vec{p}_2$ . Se trata de hallar el incremento en la cantidad de movimiento durante la colisión.

Denominamos el impulso como la integral de la fuerza respecto al tiempo en el intervalo en el que actúa

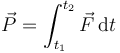
$\vec{P}=\int_{t_1}^{t_2}\vec{F}\,\mathrm{d}t$

Integrando en la segunda ley de Newton obtenemos

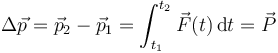
$\Delta \vec{p}=\vec{p}_2-\vec{p}_1 = \int_{t_1}^{t_2}\vec{F}(t)\,\mathrm{d}t=\vec{P}$

Es decir

“El incremento de la cantidad de movimiento es igual al impulso recibido”

Esta relación, aparentemente trivial, tiene su importancia en la teoría de colisiones y de percusiones, donde se ignora el valor exacto de la fuerza, pero sí se conoce el valor del impulso.

4 Ejemplo: colisión con una pared

Un ejemplo de impulso lo tenemos en una colisión elástica con una pared. En este caso, la fuerza actúa sobre un tiempo muy corto $ε$ , pero es capaz de producir un impulso

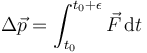
$\Delta \vec{p}=\int_{t_0}^{t_0+\epsilon}\vec{F}\,\mathrm{d}t$

Carecemos de una expresión para la fuerza (aunque se puede modelar como una fuerza elástica). Podemos determinar el impulso a partir de su efecto.

4.1 Pared estacionaria

Si tenemos una partícula de masa $m$ que impacta frontalmente con una superficie inmóvil se produce un cambio en la velocidad de la partícula, de forma que

La componente tangente a la superficie no cambia
La componente normal cambia de signo.

Supongamos que la superficie es el plano $z = 0$ . En ese caso, si la velocidad inicial es

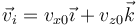
$\vec{v}_i = v_{x0}\vec{\imath}+v_{z0}\vec{k}$

la velocidad tras la colisión será

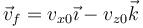
$\vec{v}_f = v_{x0}\vec{\imath}-v_{z0}\vec{k}$

siendo el impulso sobre la partícula

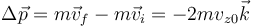
$\Delta\vec{p}=m\vec{v}_f-m\vec{v}_i=-2mv_{z0}\vec{k}$

Colisiones como esta explican el concepto de presión a nivel microscópico. Cada una de las partículas de un gas que choca contra las paredes de un recipiente transfiere una cierta cantidad de movimiento. El conjunto de todas las colisiones por unidad de tiempo es una fuerza media. La fuerza por unidad de superficie es la presión.

4.2 Pared en movimiento

Si la pared está en movimiento (caso de una raqueta que golpea una pelota), el cambio de signo se da en la velocidad relativa, no en la absoluta.

En el caso unidimensional, si la velocidad inicial de la partícula y de la pared valen

$\vec{v}_i = v_0\vec{\imath}\qquad \qquad \vec{V}=V\vec{\imath}$

la velocidad de la partícula relativa a la pared, antes de la colisión, es

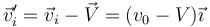
$\vec{v}'_i=\vec{v}_i-\vec{V}=(v_0-V)\vec{\imath}$

Tras la colisión, esta velocidad relativa invierte su sentido

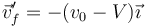
$\vec{v}'_f=-(v_0-V)\vec{\imath}$

por lo que la nueva velocidad absoluta es

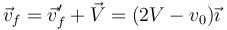
$\vec{v}_f = \vec{v}'_f+\vec{V}=(2V-v_0)\vec{\imath}$

Vemos que tras la colisión, la partícula puede moverse más o menos rápido que antes, dependiendo de ambas velocidades. En particular, si la velocidad inicial es nula, sale disparada con una velocidad doble de la raqueta, y si la velocidad inicial es el doble de la de la raqueta, tras la colisión se queda clavada en el sitio.

El impulso en esta colisión es igual a

$\Delta \vec{p}=m\vec{v}_f-m\vec{v}_i=2m(V-v_0)\vec{\imath}$

5 Teorema de conservación de la cantidad de movimiento

De la segunda ley de Newton es inmediato que:

“La cantidad de movimiento de una partícula permanece constante cuando la resultante de las fuerzas que actúan sobre ella es nula durante un intervalo de tiempo”

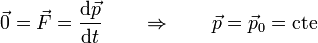
$\vec{0}=\vec{F} = \frac{\mathrm{d}\vec{p}}{\mathrm{d}t}\qquad\Rightarrow\qquad \vec{p}=\vec{p}_0=\mathrm{cte}$

Puesto que la masa de la partícula permanece constante, si la cantidad de movimiento se conserva, la velocidad también permanece constante

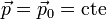
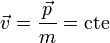
$\vec{p}=\vec{p}_0=\mathrm{cte}$ $\Rightarrow$ $\vec{v}=\frac{\vec{p}}{m}=\mathrm{cte}$

Por tanto, si la resultante de las fuerzas que actúan sobre la partícula se anula durante un intervalo de tiempo, la partícula se desplaza con un movimiento rectilíneo y uniforme durante dicho periodo.

Esto no es exactamente lo mismo que lo que dice la Primera Ley de Newton, pues esta ley habla de partícula no sometida a ninguna interacción, mientras que el teorema de conservación se refiere a una partícula sometida a diferentes fuerzas, pero tales que su resultante es nula.

Para el caso de una partícula este teorema de conservación aporta poca información nueva. Sin embargo, su extensión al caso de un sistema de partículas es extremadamente útil.

6 Conservación parcial de la cantidad de movimiento

La cantidad de movimiento es un vector, con tres componentes cartesianas. Por ello, son posibles situaciones en las que, si bien no se conserva la cantidad de movimiento en su totalidad, sí sea constante alguna de sus componentes. Concretamente:

Si la resultante de las fuerzas que actúan sobre una partícula es en todo instante perpendicular a la dirección marcada por un vector unitario $\vec{u}$ , fijo, entonces se conserva la componente en dicha dirección

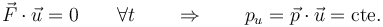
$\vec{F}\cdot\vec{u}=0\qquad\forall t\qquad\Rightarrow\qquad p_u=\vec{p}\cdot\vec{u}=\mathrm{cte.}$

Un ejemplo típico lo tenemos en el caso del movimiento por acción del peso (tiro parabólico). Al ser éste vertical en todo instante, las componentes horizontales de la cantidad de movimiento se conservan (no así la vertical).

Cantidad de movimiento (CMR)

De Laplace

Contenido

1 Definición

2 Teorema de la cantidad de movimiento

3 Impulso

4 Ejemplo: colisión con una pared

4.1 Pared estacionaria

4.2 Pared en movimiento

5 Teorema de conservación de la cantidad de movimiento

6 Conservación parcial de la cantidad de movimiento

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES