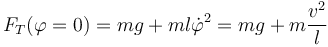Oscilaciones no lineales (CMR)

De Laplace

Revisión a fecha de 22:02 5 oct 2016; Antonio (Discusión | contribuciones)

(dif) ← Revisión anterior | Revisión actual (dif) | Revisión siguiente → (dif)

1 Oscilaciones no lineales

La ley de Hooke es aplicable a muchas situaciones en las que no tenemos un sólido elástico. Supongamos una partícula con un solo grado de libertad se encuentra sometida a una fuerza que depende de la posición $F = F (x)$ (por ejemplo, la gravitatoria o la ley de Coulomb). La partícula se encuentra en una posición de equilibrio, $x 0$ cuando la fuerza sobre ella es nula, $F (x 0) = 0$ .

Si consideramos que la partícula se encuentra en una posición próxima a $x 0$ podemos emplear, en vez de la expresión completa de $F (x)$ , que puede ser muy complicada, la serie de Taylor en torno a $x 0$

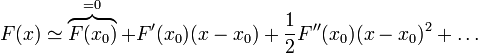
$F(x)\simeq \overbrace{F(x_0)}^{=0} + F'(x_0)(x-x_0) + \frac{1}{2}F''(x_0)(x-x_0)^2+\dots$

El equilibrio es estable cuando al separar la partícula de la posición de equilibrio, la fuerza recuperadora tiende a devolverlo a ella. En ese caso, la derivada en $x 0$ es negativa y podemos definir

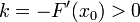
$k = -F'(x_0) > 0\,$

y la fuerza vale aproximadamente

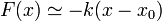
$F(x)\simeq -k(x-x_0)$

que es de nuevo la ley de Hooke. Esto nos dice que los partículas oscilan aproximadamente de forma armónica cerca de un punto de equilibrio estable.

Si nos alejamos mucho de la posición de equilibrio, ya la aproximación lineal no es suficiente y debemos recurrir a términos de orden superior. En ese caso la fuerza se aproxima por

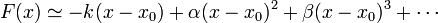
$F(x) \simeq -k(x-x_0)+ \alpha (x-x_0)^2 +\beta (x-x_0)^3+\cdots$

y ya las oscilaciones no son armónicas.

2 Péndulo simple

El ejemplo más sencillo de oscilador no lineal es el del péndulo simple. Consideremos una masa $m$ que pende de un punto fijo a través de una barra rígida ideal, sin masa, y de longitud $l$ . Por acción de la gravedad, la masa oscila en torno al punto más bajo del péndulo.

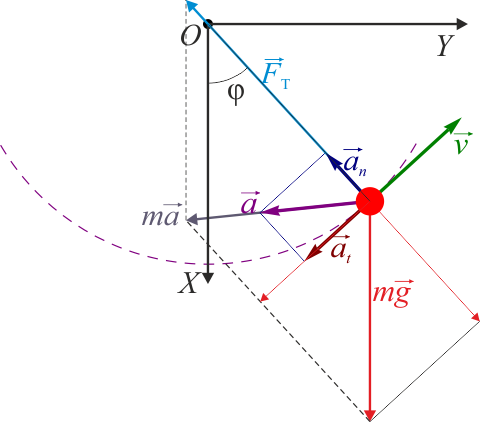
Si usamos coordenadas polares en las que $\varphi$ es el ángulo con la vertical nos quedan las ecuaciones de movimiento

$m\left(\ddot{\rho}-\rho\dot{\varphi}^2\right) = F_\rho\qquad\qquad m(\rho\ddot{\varphi}+2\dot{\rho}\dot{\varphi})=F_\varphi$

Por estar atada a una barra rígida, la distancia al centro es constante

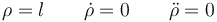
$\rho = l\qquad \dot{\rho}=0\qquad \ddot{\rho}=0$

La fuerza radial es la suma de la tensión de la barra, que va hacia adentro, con la componente radial del peso

$F_\rho = -F_T + mg\cos(\varphi)$

mientras que la fuerza acimutal contiene solo la contribución del peso

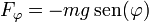
$F_\varphi = -mg\,\mathrm{sen}(\varphi)$

Esto nos deja con

$-ml\dot{\varphi}^2 = -F_T + mg\cos(\varphi)$

y

$m l \ddot{\varphi}=-mg\,\mathrm{sen}(\varphi)$

La primera ecuación nos sirve para hallar la tensión una vez que hallamos resuelto la segunda. Esta puede escribirse como

$\ddot{\varphi}=-\frac{g}{l}\mathrm{sen}(\varphi)$

Esta es la ecuación de un oscilador no lineal. Si consideramos que la lenteja del péndulo se separa poco de su posición de equilibrio

$\varphi \simeq 0\qquad\Rightarrow\qquad \mathrm{sen}(\varphi)=\varphi -\frac{\varphi^3}{6}+\cdots \simeq \varphi$

y la ecuación del péndulo se reduce a

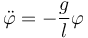
$\ddot{\varphi} = -\frac{g}{l}\varphi$

Esta es la ecuación de un oscilador armónico de frecuencia y periodo

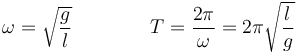
$\omega = \sqrt{\frac{g}{l}}\qquad\qquad T = \frac{2\pi}{\omega} = 2\pi\sqrt{\frac{l}{g}}$

Este resultado nos dice que, en primera aproximación, el periodo de un péndulo no depende de la amplitud de las oscilaciones (para grandes amplitudes, esto deja de ser cierto), sino solo de la longitud del péndulo.

Una vez resuelto el problema de hallar $\varphi(t)$ podemos calcular la tensión de la barra de la ecuación radial

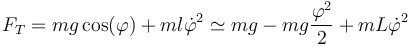
$F_T= mg\cos(\varphi) + m l\dot{\varphi}^2 \simeq mg - mg\frac{\varphi^2}{2}+mL\dot{\varphi}^2$

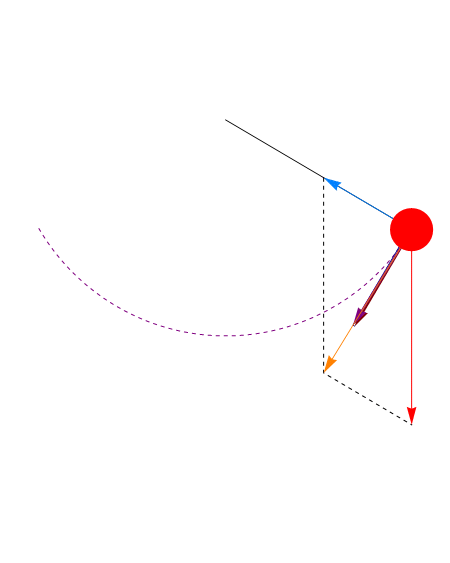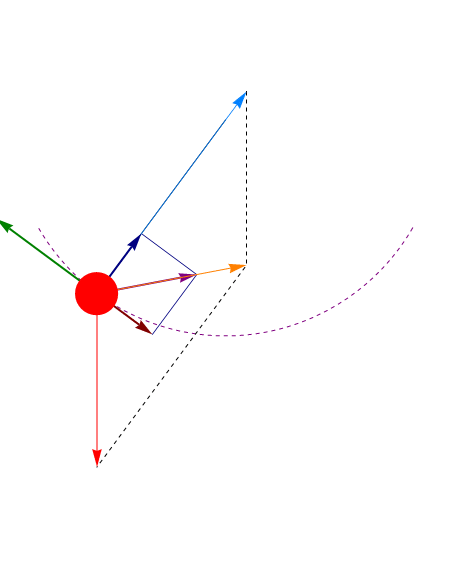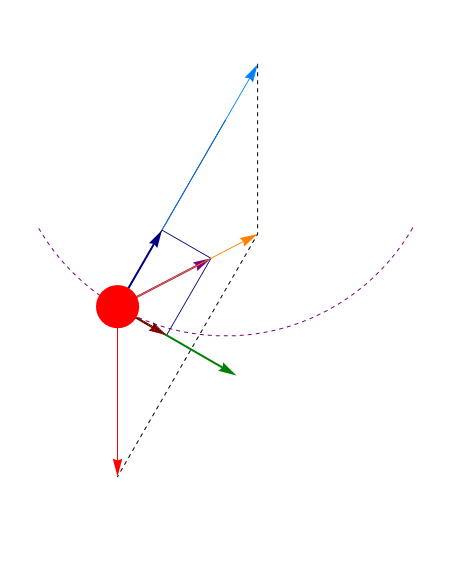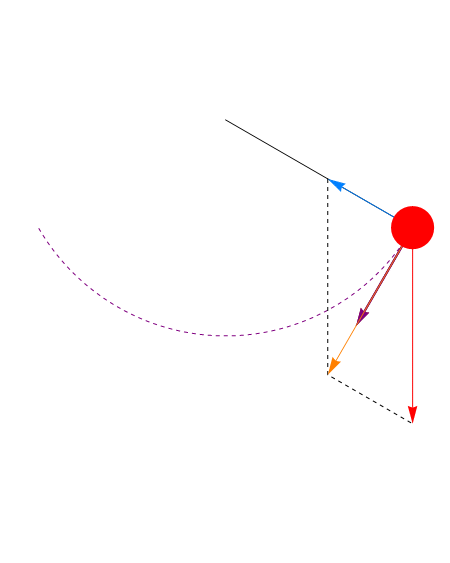
En el punto más bajo (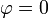 $\varphi=0$ ) esta tensión es mayor que la que habría si el péndulo estuviera en reposo, ya que la la fuerza aplicada no es nula, sino que iguala a la masa por la aceleración normal