Dinámica de la partícula y los sistemas vinculados (CMR)

De Laplace

Revisión a fecha de 09:36 25 sep 2016; Antonio (Discusión | contribuciones)

(dif) ← Revisión anterior | Revisión actual (dif) | Revisión siguiente → (dif)

Contenido

1 Definición
2 Ecuación del vínculo
3 Clasificaciones de los vínculos
4 Vínculos y grados de libertad
5 Fuerzas de reacción vincular
6 El problema de la partícula vinculada

1 Definición

Una partícula vinculada es aquella cuyo movimiento se ve restringido por una ligadura o vínculo (o enlace), de manera que no todos los puntos del espacio son accesibles.

El ejemplo más sencillo es el de una superficie, como puede ser la de una mesa, que impide que la partícula se mueva por puntos por debajo de una superficie. De la misma manera, una partícula atada a un péndulo inextensible se mueve de forma que la distancia al punto de anclaje nunca es mayor que la longitud del hilo o varilla del péndulo.

2 Ecuación del vínculo

Los vínculos o ligaduras se modelan mediante ecuaciones que relacionan las coordenadas y componentes de la posición, velocidad y posiblemente el tiempo. Típicamente un vínculo se escribirá en la forma

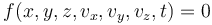
$f(x,y,z,v_x,v_y,v_z,t)= 0\,$

o si empleamos otras variables para describir la posición

$f(q_k,\dot{q}_k,t)= 0\qquad\qquad k=1,2,3$

En el caso más general, como veremos, en lugar de una igualdad hay una desigualdad. Así, por ejemplo, la existencia de una mesa horizontal en $z = 0$ hace que la posición de la partícula verifique

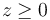
$z \geq 0\,$

De la misma manera, una masa atada a un péndulo cuyo otro extremo se encuentra en el origen de coordenadas verifica

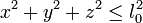
$x^2+y^2+z^2\leq l_0^2$

si se trata de un hilo flexible y

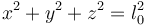
$x^2+y^2+z^2 = l_0^2$

si se trata de una varilla rígida de longitud $l 0$ .

Las ecuaciones de los vínculos se basan la mayoría de ellas en idealizaciones: hilos inextensibles, superficies absolutamente impenetrables, resistencia infinita a la tracción o compresión, etc. Por ello, en situaciones reales habrá que considerar la no idealidad de las ligaduras.

Dada la gran variedad de ligaduras posibles, es útil clasificarlas atendiendo a diferentes criterios.

3 Clasificaciones de los vínculos

3.1 Bilaterales y unilaterales

La primera división, que ya se ha mencionado, es:

Unilaterales: Impiden el movimiento en solo un sentido y se expresan mediante una desigualdad. Sería el caso de un péndulo en el que la masa pende de un hilo flexible e inextensible.

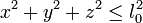
$x^2+y^2+z^2\leq l_0^2$

Bilaterales: Impiden el movimiento en ambos sentidos y se expresan mediante una igualdad. En el caso del péndulo, corresponde a que la masa cuelgue de una varilla rígida de masa despreciable.

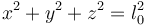
$x^2+y^2+z^2= l_0^2$

La dificultad matemática adicional que suponen los vínculos unilaterales, por ser las desigualdades más complejas de tratar analíticamente, hace que se prefiera tratar con vínculos bilaterales. Para tratar el caso unilateral, lo que se suele hacer es dividir el movimiento en intervalos. En aquellos en que el vínculo no está actuando se supone que la partícula no está sometida a él. Una vez que restringe el movimiento, se considera que es bilateral.

En el ejemplo del hilo flexible imaginemos que la masa se suelta desde una cierta altura, con el hilo destensado. Inicialmente la masa cae verticalmente. Durante ese tiempo, la partícula se considera no vinculada. Una vez que la distancia al origen coincide con la longitud del hilo, éste se tensa y la masa pasa a oscilar como lo haría un péndulo rígido. Ahora se trata como un vínculo bilateral.

Este tipo de tratamiento obliga a estudiar en qué momento del movimiento se impone el vínculo, y qué ocurre cuando se impone. Esto se modela mediante dinámica impulsiva, admitiendo que la partícula sufre una percusión.

Al igual que los vínculos se imponen, también pueden suprimirse. Sería el caso de una partícula que desliza por la superficie de una esfera. Llega un punto en que se separa de la superficie y pasa a describir un movimiento parabólico, siendo una partícula no vinculada.

3.2 Lisos y rugosos

La siguiente clasificación se refiere a la presencia de rozamiento.

Rugosos: existe rozamiento en la superficie que define el vínculo, de forma que existe una oposición al desplazamiento tangencial a ella.

Lisos: Es un tipo de vínculo ideal en el que la partícula se ve impedida en el movimiento ortogonal a la superficie que define el vínculo, pero puede moverse sin restricción en las direcciones tangenciales a ella.

3.3 Geométricos y cinemáticos

Atendiendo a las variables que aparecen en la ecuación del vínculo, tenemos:

Vínculos geométricos: Ligan exclusivamente las coordenadas de la partícula y posiblemente el tiempo.

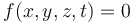
$f(x,y,z,t)=0\,$

Más en general, si la posición se expresa en términos de coordenadas generalizadas,

q k

, tendrían la forma general

$f(q_k,t)=0\qquad\qquad k=1,2,3$

Vínculos cinemáticos: incluyen también a la velocidad

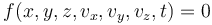
$f(x,y,z,v_x,v_y,v_z,t)=0\,$

o, en términos de las posiciones generalizadas,

q k

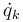, y velocidades generalizadas, $\dot{q}_k$ ,

$f(q_k,\dot{q}_k,t)=0\qquad\qquad k=1,2,3$

Aunque esta es la versión más general, en lo que sigue consideraremos exclusivamente vínculos cinemáticos que sean lineales en las velocidades generalizadas, es decir

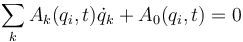
$\sum_k A_k(q_i,t)\dot{q}_k+A_0(q_i,t)=0$

Todo vínculo geométrico implica también un vínculo cinemático. Derivando en la ecuación del vínculo respecto al tiempo queda

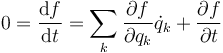
$0=\frac{\mathrm{d}f}{\mathrm{d}t}=\sum_k\frac{\partial f}{\partial q_k}\dot{q}_k+\frac{\partial f}{\partial t}$

Vemos que el resultado es una ecuación lineal en las velocidades generalizadas.

Así, por ejemplo, derivando en el vínculo del péndulo rígido

$x^2+y^2+z^2-l_0^2=0\,$

resulta que la velocidad de la lenteja debe ser perpendicular a la varilla

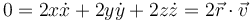
$0 = 2x\dot{x}+2y\dot{y}+2z\dot{z}=2\vec{r}\cdot\vec{v}$

El recíproco a la relación anterior no es cierta, en general: de todo vínculo cinemático no se deduce un vínculo geométrico.

3.4 Holónomos y no holónomos

Relacionado con lo anterior, se establece la siguiente distinción:

Vínculo holónomo: es aquél que, o bien es un vínculo geométrico o siendo cinemático puede integrarse para obtener uno geométrico.
Víncluo no holónomo: Es aquél vínculo cinemático que no se puede integrar para dar uno geométrico.

Aquí, que “no se puede integrar” no significa que resulte una integral muy complicada o imposible de hallar analíticamente, sino que es imposible llegar siquiera a plantear una integral.

Por ejemplo, el vínculo cinemático

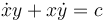
$\dot{x}y+x\dot{y}=c$

es holónomo porque puede integrarse. El primer miembro es la derivada temporal de un producto, así que podemos integrar en cada miembro y llegar al vínculo geométrico

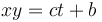
$xy=ct+b\,$

En cambio, el vínculo cinemático aparentemente muy similar

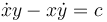
$\dot{x}y-x\dot{y}=c$

es no integrable y no conduce a un vínculo geométrico. Este sería no holónomo.

El caso más importante de vínculo no holónomo que encontraremos más adelante es el de la rodadura sin deslizamiento de un sólido, para el cual la velocidad en el punto de contacto es nula, pero de ahí no se deduce una relación explícita entre las coordenadas.

3.5 Esclerónomos y reónomos

Esta clasificación se refiere a la aparición explícita del tiempo en el vínculo.

Vínculos esclerónomos: son aquellos en que no aparece explícitamente el tiempo, es decir, se trata de ligaduras que imponen la misma condición en todo instante

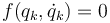
$f(q_k,\dot{q}_k)=0\,$

Vínculos reónomos: son los no esclerónomos, es decir, el tiempo aparece en la ecuación del vínculo

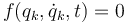
$f(q_k,\dot{q}_k,t)=0$

En el ejemplo del péndulo, la ecuación que hemos escrito antes es un vínculo esclerónomo

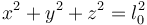
$x^2+y^2+z^2 = l_0^2\,$

pero imaginemos que el péndulo cuelga no de un punto fijo sino de un vibrador que oscila verticalmente. En ese caso la ecuación del vínculo sería reónoma

$x^2+y^2+\left(z-b\cos(\Omega t)\right)^2 = l_0^2\,$

4 Vínculos y grados de libertad

Una partícula puede estar sometida a verios vínculos simultáneamente. Así, por ejemplo, una masa atada al extremo de una varilla cuyo otro extremo está fijo y que se ve obligada a oscilar en un plano vertical dado cumple simultáneamente

$\left\{\begin{array}{rcl} y& = & 0 \\ x^2+y^2+z^2 & = & l_0^2 \end{array}\right.$

o equivalentemente

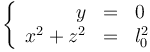
$\left\{\begin{array}{rcl} y& = & 0 \\ x^2+z^2 & = & l_0^2 \end{array}\right.$

es decir, cuando hay varios vínculos presentes, estos pueden combinarse de diferentes maneras para producir el mismo efecto.

La presencia de uno o varios vínculos implica una reducción en los movimientos posibles, y por tanto, reducen los grados de libertad de la partícula en tantos como vínculos haya, es decir

$\mathrm{GL}=3-r\,$

siendo $r$ el número de vínculos independientes (ya que podrían ser redundantes).

Así, la partícula suspendida del péndulo rígido tiene 2 GDL. Si simultáneamente se lo obliga a oscilar sobre un plano vertical tiene 1 GDL. Si además ahora sujetamos la masa con otra varilla resultan 0 GDL. En ese momento ya la partícula no puede moverse de ninguna forma.

Cuando todos los vínculos son holónomos, podemos, en teoría, elegir un sistema de $3 - r$ coordenadas generalizadas que satisfaga automáticamente los vínculos, eliminándolos del problema.

Así, para el péndulo rígido, podemos usar coordenadas esféricas(ya que la partícula está obligada a moverse sobre la superficie de una esfera de centro el punto de anclaje y de radio la longitud de la varilla)

$\begin{array}{rcl}x & = & l_0\,\mathrm{sen}(\theta)\cos(\varphi)\\ y & = & l_0\,\mathrm{sen}(\theta)\,\mathrm{sen}(\varphi) \\ z & = & l_0\cos(\theta)\end{array}$

siendo solo θ y φ las coordenadas dependientes del tiempo.

Si además la masa está obligada a moverse verticalmente podemos fijar una coordenada y reducir el problema a una sola variable

$\begin{array}{rcl}x & = & l_0\,\mathrm{sen}(\theta)\\ y & = & 0 \\ z & = & l_0\cos(\theta)\end{array}$

Si además la masa se fija con otra varilla, determinamos el valor de θ y desaparece la dependencia temporal.

Por ello, en muchos problemas, el que la partícula tenga $3 - r$ grados de libertad equivale al estudio de $3 - r$ variables. Sin embargo, ello no siempre es posible. Si existen vínculos no holónomos, la ecuación de estos no puede recucirse a una relación entre las coordenadas, por lo que es necesario trabajar con todas ellas, aunque permanezcan vinculadas. En general, el número de grados de libertad no equivale al número de coordenadas independientes.

5 Fuerzas de reacción vincular

6 El problema de la partícula vinculada

Dinámica de la partícula y los sistemas vinculados (CMR)

De Laplace

Contenido

1 Definición

2 Ecuación del vínculo

3 Clasificaciones de los vínculos

3.1 Bilaterales y unilaterales

3.2 Lisos y rugosos

3.3 Geométricos y cinemáticos

3.4 Holónomos y no holónomos

3.5 Esclerónomos y reónomos

4 Vínculos y grados de libertad

5 Fuerzas de reacción vincular

6 El problema de la partícula vinculada

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES