Dinámica de la partícula y los sistemas vinculados (CMR)
De Laplace
Contenido |
1 Definición
Una partícula vinculada es aquella cuyo movimiento se ve restringido por una ligadura o vínculo (o enlace), de manera que no todos los puntos del espacio son accesibles.
El ejemplo más sencillo es el de una superficie, como puede ser la de una mesa, que impide que la partícula se mueva por puntos por debajo de una superficie. De la misma manera, una partícula atada a un péndulo inextensible se mueve de forma que la distancia al punto de anclaje nunca es mayor que la longitud del hilo o varilla del péndulo.
2 Ecuación del vínculo
Los vínculos o ligaduras se modelan mediante ecuaciones que relacionan las coordenadas y componentes de la posición, velocidad y posblemente el tiempo. Típicamente un vínculo se escribirá en la forma
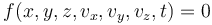
o si empleamos otras variables para describir la posición

En el caso más general, como veremos, en lugar de una igualdad hay una desigualdad. Así, por ejemplo, la existencia de una mesa horizontal en z = 0 hace que la posición de la partícula verifique
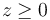
De la misma manera, una masa atada a un péndulo cuyo otro extremo se encuentra en el origen de coordenadas verifica
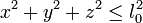
si se trata de un hilo flexible y
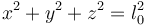
si se trata de una varilla rígida de longitud l0.
Las ecuaciones de los vínculos se basan la mayoría de ellas en idealizaciones: hilos inextensibles, superficies absolutamente impenetrables, resistencia infinita a la tracción o compresión, etc. Por ello, en situaciones reales habrá que considerar la no idealidad de las ligaduras.
Dada la gran variedad de ligaduras posibles, es útil clasificarlas atendiendo a diferentess criterios.





