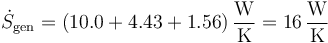Frigorífico alimentado por un generador
De Laplace
Contenido |
1 Enunciado
En una casa de campo se tiene un frigorífico cuya temperatura interior es de 3 °C siendo la exterior de 27 °C. En el estado estacionario, a través de las paredes circula un flujo de calor de 5.4kWt. El COPR del frigorífico vale 3. Para hacer funcionar la nevera se usa un generador de gasoil que tiene un rendimiento del 30% y en el cual el combustible alcanza la temperatura de 1500K. El poder calorífico del gasoil empleado es de 36 MJ por cada litro de combustible.
- Calcule el flujo de trabajo (potencia) necesario para mantener en funcionamiento la máquina frigorífica.
- Halle el flujo de calor que debe producirse en la combustión dentro del generador para generar la potencia que necesita la máquina frigorífica.
- Calcule el consumo de gasoil, en litros, a lo largo de un día para mantener el sistema en funcionamiento.
- Determine la producción de entropía por segundo en el generador, en la máquina frigorífica del refrigerador y en la cámara frigorífica, así como la producción total de entropía por segundo.
2 Introducción
Los cálculos de este problema, como veremos, son muy simples. La principal dificultad está en tener claro dónde entra y dónde sale el calor y el trabajo.
El sistema se compone de tres partes:
- Una cámara frigorífica (CF)
- en la cual entra desde el exterior (porque está más caliente) un flujo de calor
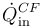 , cuyo valor conocemos (5.4 kW).
, cuyo valor conocemos (5.4 kW).
- Una máquina frigorífica (MF)
- para mantener la temperatura interior, ese calor debe ser extraído, de lo cual se encarga la máquina frigorífica (compresor, condensador,…). Esta máquina toma ese calor y expulsa de nuevo al exterior aunque, de acuerdo con el enunciado de Clausius, para hacerlo requiere una cierta cantidad de trabajo. Tenemos entonces que
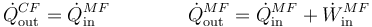
- Una máquina térmica (MT)
- El trabajo para hacer funcionar la máquina frigorífica no sale de la red eléctrica, sino que la proporciona un generador de gasoil. Éste funciona como una máquina térmica en la cual el calor se toma de la combustión y parte se emplea en realizar el trabajo requerido y parte se va en calor de desecho. Tenemos entonces
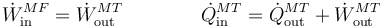
Esquemáticamente, sería lo siguiente:
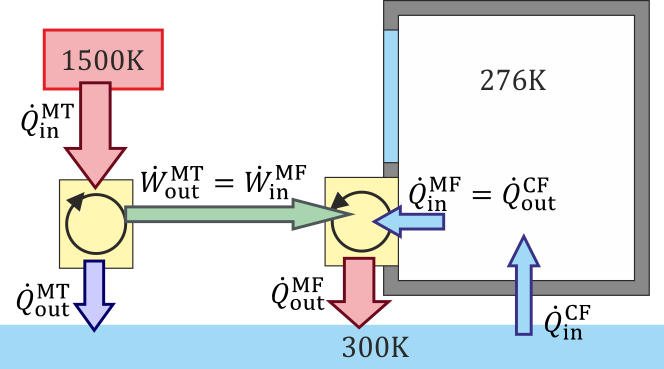
3 Potencia
Para mantener el estado estacionario, el calor que entra en la cámara frigorífica desde el exterior debe ser compensado por el que sale de ella gracias a la máquina frigorífica
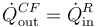
Por tanto, el flujo de calor que entra en la máquina frigorífica es
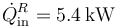
El coeficiente de desempeño de un refrigerador, por definición, es igual a
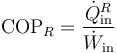
y por tanto, la potencia necesaria para hacer funcionar el refrigerador es

4 Flujo de calor
La potencia del apartado anterior es suministrada por un generador

siendo el rendimiento un 30%, por tanto,
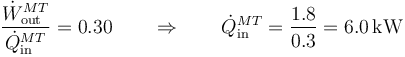
5 Consumo de combustible
El resultado anterior indica que se precisan 6 kJ/s de calor. A lo largo de un día se necesitarán
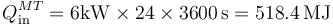
Si cada litro aporta 36MJ el consumo será
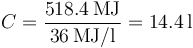
6 Producción de entropía
El resumen de todos los flujos y temperaturas es el de la siguiente figura:
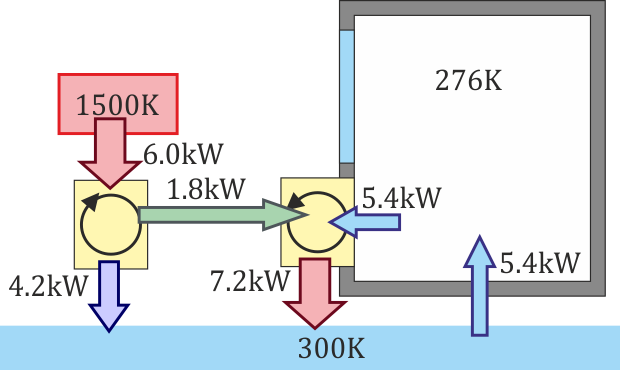
Salvo el flujo de trabajo del generador a la máquina frigorífica, todos los demás son flujos de calor.
6.1 En el generador
El generador toma cada segundo 6kJ a 1500K y expulsa (6-1.8)kJ = 4.2kJ a 300K por tanto su producción de entropía es

6.2 En la máquina frigorífica
La máquina frigorífica extrae 5.4kW a 276K y vierte (5.4+1.8)kW = 7.2kW a 300K. Por tanto genera la entropía
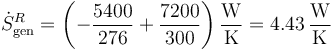
6.3 En la cámara frigorífica
En la cámara salen 5.4kW del ambiente a 300K y entran en la cámara a 276K, por lo que en la cámara se genera
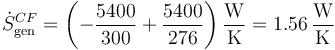
6.4 Producción total de entropía
Sumamos las tres contribuciones anteriores