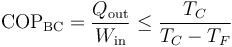Teorema de Carnot para una bomba de calor
De Laplace
Contenido |
1 Cuestión
Enuncie el Teorema de Carnot para el coeficiente de desempeño de una bomba de calor.
¿Entre qué valores está comprendido el COP para una bomba de calor que caldee una habitación a 24 °C estando el exterior a 3 °C?
Demuestre razonadamente este teorema partiendo de alguno de los otros enunciados del segundo principio de la termodinámica.
2 Enunciado del teorema
El Teorema de Carnot para una bomba de calor puede enunciarse como:
- El coeficiente de desempeño de una bomba de calor es siempre menor o igual que el de una bomba de calor reversible que opere entre las temperaturas extremas del ciclo.
Matemáticamente sería
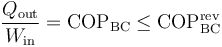
donde el coeficiente de desempeño de una bomba de calor reversible es

con TC la temperatura del foco caliente (la habitación a caldear) y TF la del foco frío (el ambiente).
3 Valores límite
Para los valores del enunciado, el COP máximo es
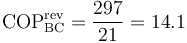
Puest que el COP de una bomba de calor vale como mínimo la unidad, queda el rango
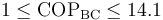
4 Demostración del teorema
Para demostrar el enunciado puede partirse de cualquiera de las versiones del segundo principio. Dado que todas son equivalentes, con que se demuestre con una es suficiente.
Una forma sencilla es partiendo del aumento de entropía, que nos dice que si tenemos un sistema experimenta un proceso real se cumple
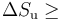
En el caso de un proceso cíclico, la entropía del sistema no cambia, por ser una función de estado. Solo cambia la del ambiente.
La variación de entropía del aumente consta de una reducción en el foco frío (de donde sale el calor que entr en la bomba) y un aumento de la del foco caliente (donde se expulsa el calor que sale de la bomba), esto es
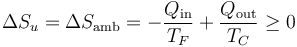
Aplicamos que
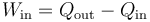
y queda
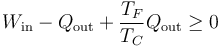
o lo que es lo mismo

y finalmente