No Boletín - Cuestión sobre tres velocidades (Ex.Feb/14)
De Laplace
Contenido |
1 Enunciado
Las posiciones y velocidades instantáneas de tres puntos de un sólido rígido vienen dadas por:
| Punto |  (m) (m)
|  (m/s) (m/s)
|
|---|---|---|
| A | 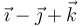
| 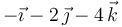
|
| B | 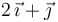
| 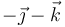
|
| C | 
| 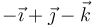
|
¿Cuál de las siguientes afirmaciones es verdadera?
(a) Estos datos son incompatibles con la rigidez
(b) La velocidad de deslizamiento (segundo invariante) vale 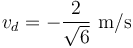
(c) La velocidad angular (primer invariante) vale 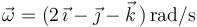
(d) El eje instantáneo de rotación pasa por el punto de coordenadas 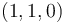
2 Equiproyectividad. Descartando (a)
La condición cinemática de rigidez consiste en la equiproyectividad del campo de velocidades:
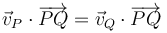
Sometiendo a examen a cada par de puntos:
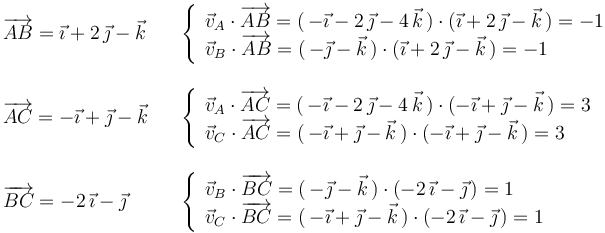
Queda comprobado que los datos del enunciado son compatibles con la rigidez, y por tanto la afirmación (a) es FALSA.
3 Cálculo de la velocidad angular. Descartando (c)
Podemos deducir el vector velocidad angular 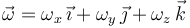 del sólido, componente a componente, exigiendo el cumplimiento de la ecuación del campo de velocidades en la relación entre las velocidades conocidas.
del sólido, componente a componente, exigiendo el cumplimiento de la ecuación del campo de velocidades en la relación entre las velocidades conocidas.
Por ejemplo, la relación entre 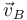 y
y 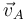 debe satisfacer la ecuación:
debe satisfacer la ecuación:
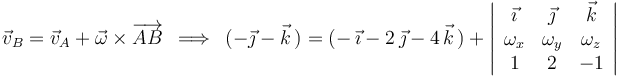
E igualando componentes homólogas:
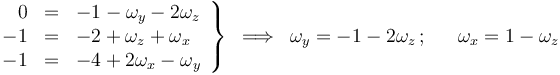
Y relacionando de forma análoga 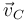 y
y 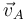 , podemos culminar la deducción de
, podemos culminar la deducción de 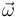 :
:
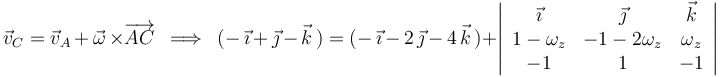
E igualando componentes homólogas:

Por tanto, el vector velocidad angular (primer invariante) es:
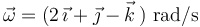
Puede observarse que el valor de 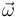 obtenido no coincide con el propuesto en la afirmación (c). En concreto, la discrepancia está en el signo de la segunda componente. Por tanto, la afirmación (c) es FALSA.
obtenido no coincide con el propuesto en la afirmación (c). En concreto, la discrepancia está en el signo de la segunda componente. Por tanto, la afirmación (c) es FALSA.
4 Cálculo de la velocidad de deslizamiento. Descartando (b)
La velocidad de deslizamiento 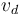 (segundo invariante) es la proyección de la velocidad de cualquier punto (por ejemplo,
(segundo invariante) es la proyección de la velocidad de cualquier punto (por ejemplo,  ) sobre la dirección de la velocidad angular:
) sobre la dirección de la velocidad angular:
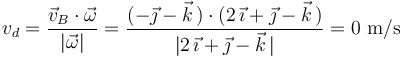
El hecho de que el segundo invariante sea nulo (siendo no nulo el primer invariante) implica que el movimiento analizado en este ejercicio se describe canónicamente como una rotación pura. Puede observarse que el valor obtenido de 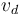 no coincide con el propuesto en la afirmación (b). Por tanto, la afirmación (b) es FALSA.
no coincide con el propuesto en la afirmación (b). Por tanto, la afirmación (b) es FALSA.
5 El EIR pasa por el punto (1,1,0). Eligiendo (d)
Sabemos ya que el movimiento analizado es una rotación (primer invariante no nulo y segundo invariante nulo), y que por tanto existe un eje instantáneo de rotación (EIR), el cual es el lugar geométrico de los puntos que tienen velocidad instantánea nula. Denominando  al punto de coordenadas
al punto de coordenadas 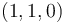 , podemos verificar su pertenencia al EIR comprobando que su velocidad es en efecto nula:
, podemos verificar su pertenencia al EIR comprobando que su velocidad es en efecto nula:
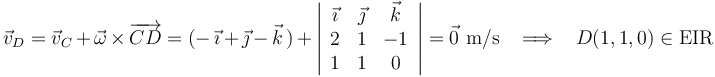
Por tanto, la afirmación (d) es VERDADERA y constituye la respuesta correcta a la pregunta formulada en el enunciado.





